Нечеткая логика применяется в системах автоматического управления для различных целей и условно можно выделить две области ее практической реализации:
· нечеткие логические регуляторы, которые функционируют в прямом контуре и выполняют функции некоторого линейного преобразователя, в том числе они могут реализовывать линейные функции по типу П, ПИ, ПИД и др. регуляторов;
· комбинированные нечеткие регуляторы, у которых в прямом контуре функционируют традиционные регуляторы, а в дополнительном контуре имеются нечеткие системы, которые адаптируют коэффициенты усиления регулятора прямого контура, подстраивая их к изменяющимся условиям функционирования объекта управления. Ниже приводятся примеры нескольких таких систем нечеткого логического управления.
4.1. Нечеткое логическое управление подъемно-транспортным механизмом [5].
При управлении сложными нелинейными объектами обычно используется два подхода. При первом пытаются описать объект с помощью различных математических моделей. Однако, в эти модели входит достаточно много эмпирических коэффициентов, которые, как правило, изменяются в широком диапазоне и их идентификация является сложной научно технической задачей. Кроме того, возникают проблемы обеспечения устойчивости вычислительного процесса.
При таком подходе системы управления не обеспечивают нужного качества управления и, как следствие этого, не удается получить готовую продукцию с высокими потребительскими свойствами. Примерами таких объектов являются доменная печь в металлургии, ректификационная колонна при переработке нефти и т.д.
Однако с управлением такими сложными объектами человек справляется достаточно уверенно. При этом он использует показания контрольно-измерительных приборов и по эвристическим алгоритмам, которые основаны на опыте и интуиции, воздействует на исполнительные органы объекта, добиваясь приемлемых конечных результатов. При этом, чем более квалифицирован оператор, тем лучших результатов он добивается. В этой связи возможен второй подход при управлении сложными объектами, когда эвристические алгоритмы управления реализуются с использованием языка нечеткой логики, который по своей структуре близок к естественному языку. Впервые этот подход в виде нечеткой системы управления был реализован при управлении цементной печью.
Ниже дается простейший пример нечеткого управления подъемно-транспортным механизмом, когда на специализированном языке формализуются действия оператора для предотвращения раскачивания груза на крюке подъемно-транспортного механизма при начале его перемещения, изменении скоростных режимов или остановке.
Покажем предварительно, что объект, которым управляет крановщик является нелинейным динамическим объектом. Простейшей одномерной математической моделью раскачивания груза при движении крана является маятник с подвижной точкой подвеса (рис.4.1) Баланс моментов относительно точки О дает
M1+M2=M3,
где 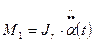 - момент инерции груза относительно точки подвеса;
- момент инерции груза относительно точки подвеса;
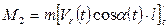 - момент, создаваемый составляющей скорости подвеса, относительно точки подвеса;
- момент, создаваемый составляющей скорости подвеса, относительно точки подвеса;
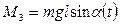 -момент, создаваемый составляющей веса груза, относительно точки подвеса. После интегрирования и преобразований получим:
-момент, создаваемый составляющей веса груза, относительно точки подвеса. После интегрирования и преобразований получим:
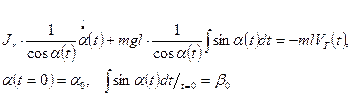
- начальные условия нелинейного интегро-дифференциального уравнения.
Задача управления нелинейным объектом состоит в определении скорости V0(t) по измерениям его текущей скорости VТ(t) и угла раскачивания a(t) для того, чтобы предотвратить опасное раскачивание груза при изменении скоростных режимов крана (рис.4.2): начало разгона - т.О1; конец разгона т.О2; начало торможения т.О3; конец торможения т.О4. Эта задача решается оператором крана эвристическим способом. Один из возможных вариантов изменения скорости V0(t) в конце торможения (т.О4.), при котором обеспечивается.2): начало разгона- т.О1; конец разгона т.О2; начало торможения т.О3; конец торможения т.О4. Эта задача решается оператором крана эвристическим способом. Один из возможных вариантов изменения скорости V0(t) в конце торможения (т.О4.), при котором обеспечивается.2): начало разгона- т.О1; конец разгона т.О2; начало торможения т.О3; конец торможения т.О4. Эта задача решается оператором крана эвристическим способом. Один из возможных вариантов изменения скорости V0(t) в конце торможения (т.О4.), при котором обеспечивается min a(t), показан на рис 4.3. При этом оператор формулирует для себя одно из возможных лингвистических правил:
Ri: если угол da =a3-a, где a3 - задание, a - измеренное значение; немного увеличивается по часовой стрелке и производная угла 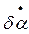 колебания груза немного увеличивается против часовой стрелки и скорость dVT= VTЗ - VT, где VTЗ – задание, VT – измеренное значение; равна нулю, тогда скорость V0 должна быть небольшой в отрицательном направлении относительно нуля.
колебания груза немного увеличивается против часовой стрелки и скорость dVT= VTЗ - VT, где VTЗ – задание, VT – измеренное значение; равна нулю, тогда скорость V0 должна быть небольшой в отрицательном направлении относительно нуля.
Определим для нечетких лингвистических переменных da, 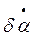 , dVT, V0 нечеткие множества с соответствующими идентификаторами для функций принадлежностей m(da),m(
, dVT, V0 нечеткие множества с соответствующими идентификаторами для функций принадлежностей m(da),m(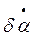 ), m(VT), m(V0) (рис.4.4). Например, для m(da) эти идентификаторы имеют вид:
), m(VT), m(V0) (рис.4.4). Например, для m(da) эти идентификаторы имеют вид:
PM- угол раскачивания da положительный (против часовой стрелки) средний;
PS- угол раскачивания da положительный небольшой;
ZR - угол раскачивания da нулевой;
NS - угол раскачивания da отрицательный (по часовой стрелки) небольшой;
NM - угол раскачивания da отрицательный средний.
|
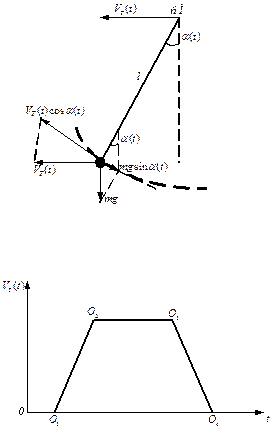
|


|
Аналогично определяются идентификаторы для m(da), m(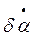 ), m(V0).
), m(V0).
С учетом заданных нечетких множеств база правил эвристического алгоритма управления оператором скоростью V0(t) крана при VТ(t) =0(т.О4, рис.4.2) имеет вид:
R1: если da=NS и 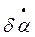 =NS и dVT=ZR, тогда V0=ZR
=NS и dVT=ZR, тогда V0=ZR
или
R2: если da=NS и 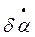 =ZR и dVT=ZR, тогда V0=NS
=ZR и dVT=ZR, тогда V0=NS
или
R3: если da=NS и 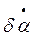 =PS и dVT=ZR, тогда V0=NS
=PS и dVT=ZR, тогда V0=NS
или
{R  }
}  R
R 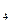 : если
: если 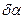 =ZR и
=ZR и 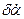 =NS и
=NS и 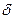 V
V 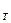 =ZR, тогда V
=ZR, тогда V 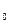 =PS
=PS
R5: если da=ZR и 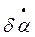 =ZR и dVT=ZR, тогда V0=ZR
=ZR и dVT=ZR, тогда V0=ZR
или
R6: если da=ZR и 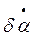 =PS и dVT=ZR, тогда V0=NS
=PS и dVT=ZR, тогда V0=NS
или
R7: если da=PS и 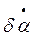 =NS и dVT=ZR, тогда V0=PS.
=NS и dVT=ZR, тогда V0=PS.
Аналогичные базы правил могут быть записаны для т.т. О1-О3 изменения скоростных режимов крана (рис.4.2). После их объединения получим формализованное представление эвристического алгоритма, с помощью которого оператор управляет скорость перемещения крана для предотвращения опасного раскачивания груза. Реализация этого алгоритма в виде нечеткого контроллера в прямом контуре управления позволяют исключить оператора крана и передать его функции нечеткой системе регулирования.
Приведенный пример показывает преимущество нечеткой системы регулирования нелинейным объектом по сравнению с традиционной системой регулирования простотой своей технической реализации. Блок схема нечеткой системы регулирования изображена на рис.4.5. Подобные нечеткие системы регулирования могут быть рассмотрены для подъемно-транспортных механизмов загрузки ракет в подводные лодки, шахты, на пусковые платформы и т.д. с учетом воздействия неконтролируемых факторов типа: ветровые нагрузки, которые воздействуют на груз; волнения поверхности воды, которые перемещают место расположения посадки ракеты и т.д. Во всех этих случаях действия опытного оператора могут быть формализованы и далее реализованы в виде нечеткой системы регулирования.

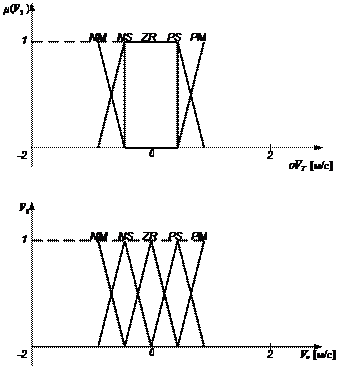
|
4.2. Нечеткое логическое управление температурой химического реактора [5].
Нечеткое управление применяется для поддержания температуры внутри «рубашки» химического реактора, сделанного по принципу термоса (рис.4.6). Химические реакторы такого типа используются в медицине, химии, в производстве косметики и т.д., когда необходимо обеспечить плавность изменения температуры во времени и одновременно равномерность ее изменения внутри реактора.
Температура внутри реактора управляется путем изменения температуры рабочего тела внутри «рубашки» реактора. При управлении по классической схеме обычно используется ПИД-регулятор. Однако, использование нечеткого управления может повысить точность регулирования, обеспечивая таким способом выход более качественной продукции.
Основная задача управления состоит в поддержании заданной температуры внутри реактора, которая может изменяться под воздействием неконтролируемых возмущений. Например, в результате добавления материала 1 в реактор может происходить химическая реакция с выделением или поглощением тепла, поэтому необходимо соответственно либо понижать, либо повышать температуру внутри «рубашки», быстро восстанавливая заданную температуру внутри реактора. Метод управления с использованием ПИД-регулятора не может обеспечить автоматическое решение этой задачи из-за воздействия неконтролируемых возмущений. Как правило, при таком способе управления, оператор визуально контролирует температуру и затем изменяет задание ПИД-регулятора по режимным картам. Однако использование в системе управления блока обработки нечетких высказываний позволяет полностью автоматизировать процедуру текущей настройки ПИД-регулятора. Проблемы управления, результат и эффективность нечеткого управления представлены в таблице 4.2.
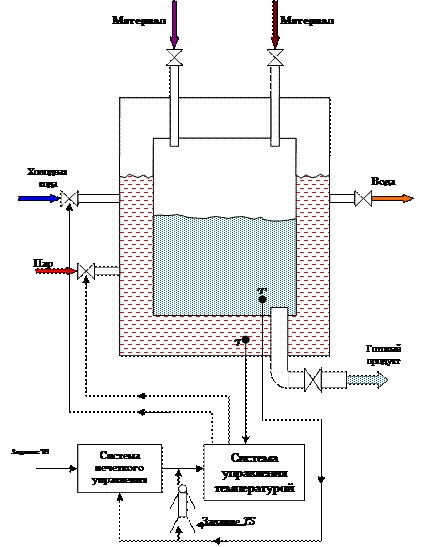
Рис. 4.6. Система управления температурой химического реактора (жирные стрелки – классический контур управления температурой).

Рис.4.7. Блок-схема системы нечеткого управления температурой химического реактора.

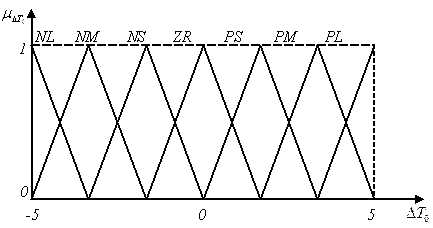
Рис.4.8. Функции принадлежностей для входных и выходных переменных системы нечеткого управления температурой химического реактора.
Таблица 4.2.
| Постановка задачи Управления | Результат при улучшении управления | Эффективность нечеткого управления |
| Из-за неконтролируемых возмущений возможно появление выбросов температуры, которую необходимо стабилизировать. Настройка для изменения температуры должна быть сделана автоматически, без участия оператора. | Исключаются выбросы температуры и обеспечивается точное ее поддержание. | Качественное отслеживание заданных температурных графиков. |
| Снижение требований к квалификации оператора. | Упрощение процесса управления с помощью оператора. | |
| Не существует формализованных правил настройки регулятора к требуемой температуре. | Использование для формализации нечетких высказываний. |
Блок-схема нечеткого управления температурой реактора показана на рис.4.7. Имеется задание на температуру внутри химического реактора ТS. С помощью датчика измеряется Т- текущая температурареактора и преобразуется в цифровое значение. Вычисляется отклонение 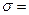 TS-T и производная
TS-T и производная 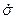 (приращение
(приращение 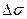 ).
).
В зависимости от величин 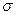 и
и 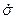 корректируется температура Т
корректируется температура Т 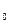 - «рубашки» реактора путем воздействия на заслонки холодной воды и пара.
- «рубашки» реактора путем воздействия на заслонки холодной воды и пара.
Функции принадлежностей для переменных 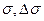 и
и 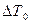 показаны на рис.4.8. Правило нечеткого высказывания имеет два условия
показаны на рис.4.8. Правило нечеткого высказывания имеет два условия 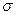 и
и 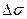 , соединенных логическим «и» и одно заключение
, соединенных логическим «и» и одно заключение 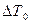 , т.е. система нечеткого управления имеет два входа и один выход. Каждая функция принадлежностей для входных переменных имеет 7 меток: { NL, NM,... NL } .
, т.е. система нечеткого управления имеет два входа и один выход. Каждая функция принадлежностей для входных переменных имеет 7 меток: { NL, NM,... NL } .
Для 2-х условий и 7-ми меток для каждой входной переменной имеется 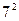 =49 возможных комбинаций, что соответствует 49 правилам. Эти правила изображены ниже в виде матрицы:
=49 возможных комбинаций, что соответствует 49 правилам. Эти правила изображены ниже в виде матрицы:
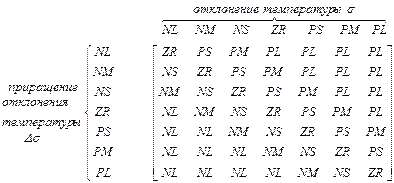
В этой матрице элемент с координатами (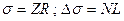 ) является пустым, т.к. условие правила:
) является пустым, т.к. условие правила:
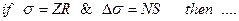
соответствует наличию шума на выходе объекта управления. Для простых систем управления типа «2 входа и 1 выход», элементы матрицы задаются с автономного дисплея, входящего в состав технических средств.
Программа нечеткого контроллера может быть написана в терминах «if – then» с использованием матрицы. Например, одно из правил:
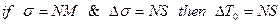
4.3. Нечеткая логическая настройка скорости двух транспортеров[5].
В этом примере нечеткое управление обеспечивает синхронное управление двумя транспортными конвейерами в ходе упаковки изделий при их нерегулярном потоке (рис.4.9).
Объект управления состоит из двух транспортеров A и B. Транспортер A перемещает изделия, а транспортер B – упаковочные коробки для изделий. Потоки изделий и коробок не являются регулярными по времени. Оба транспортера имеют фотодатчики PH1 - PH4, которые обнаруживают наличие изделий и коробок. Задача управления состоит в синхронизации транспортера B, обеспечивающего встречу изделия и его упаковочной коробки. Подобная задача имеет место и при сборке автомобилей при помощи роботов, автоматической сборке электронных плат и т.д.
Блок-схема алгоритма системы нечеткого управления представлена на рис.4.10. С помощью фотодатчиков PH1 и PH3 обнаруживаются предметы на транспортерах A и B конвейера и регистрируется начало отсчета времени.
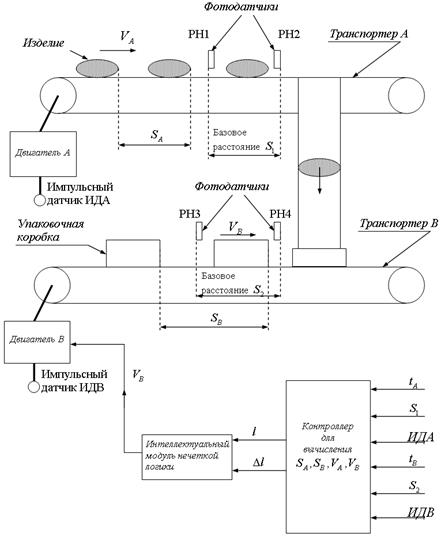
Рис.4.9. Функциональная схема конвейера с двумя транспортерами и система нечеткого управления ими.

Рис.4.10. Блок-схема системы нечеткого управления скоростью транспортера конвейера.
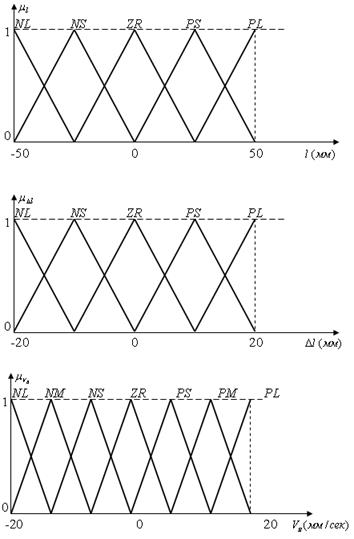
Рис.4.11. Функции принадлежностей для входных и выходных переменных системы нечеткого управления настройкой транспортеров конвейера.
При прохождении этими предметами базовых расстояний определяются текущие скорости 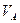 и
и 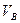 транспортеров. С помощью импульсных датчиков ИДА и ИДВ, установленных на двигателях A и B, определяются расстояния между предметами
транспортеров. С помощью импульсных датчиков ИДА и ИДВ, установленных на двигателях A и B, определяются расстояния между предметами 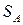 и
и 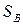 . По этим величинам находится отклонение
. По этим величинам находится отклонение 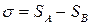 , определяется разность
, определяется разность 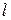 в перемещениях транспортеров А и В, и вычисляется ее первая производная
в перемещениях транспортеров А и В, и вычисляется ее первая производная 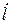 .
.
По величинам 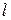 и
и 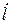 , являющимся условиями нечеткого высказывания, происходит его исполнение «if / then» и задается необходимая скорость
, являющимся условиями нечеткого высказывания, происходит его исполнение «if / then» и задается необходимая скорость 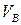 транспортера В. Таким образом, система нечеткого управления имеет два входа и один выход. Функции принадлежностей изображены на рис.4.11. Для входных переменных используется пять меток: { NL, NS, …, PL }, а для выходной переменной семь меток: { NL, NM, …, PL }.
транспортера В. Таким образом, система нечеткого управления имеет два входа и один выход. Функции принадлежностей изображены на рис.4.11. Для входных переменных используется пять меток: { NL, NS, …, PL }, а для выходной переменной семь меток: { NL, NM, …, PL }.
Программа для нечеткого контроллера задается в виде матрицы:
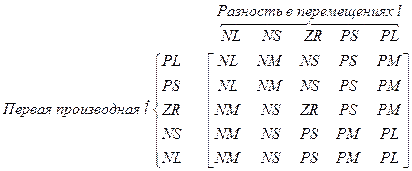
Одно из правил, соответствующее элементу в 4-й строке и 2-м столбце матрицы, приведено ниже:
if 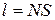 &
& 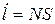 then
then 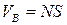 .
.
4.4. Гибридные системы управления [5].
Рассмотрим традиционную систему регулирования для асинхронного электропривода с частотным преобразователем и далее модифицируем ее с использованием нечетких высказываний. Как будет показано далее, это дает улучшение динамических характеристик (пуск, торможение) и точность поддержания задания асинхронного двигателя.
|
|

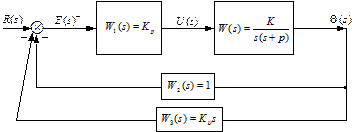
|
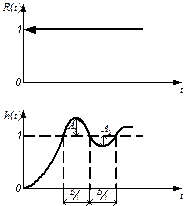
|
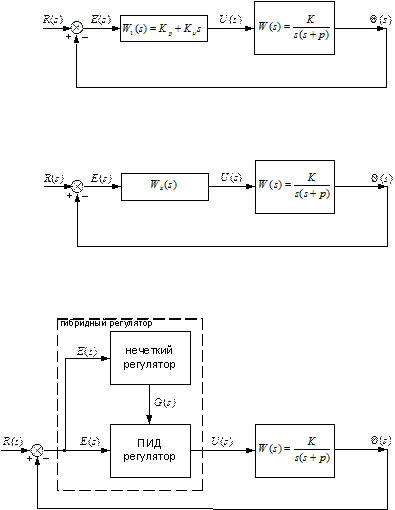
Рассмотрим структурную схему 1 классической системы с ПД регулятором в цепи обратной связи и проанализируем ее эффективность (рис.4.12). На схеме приняты следующие обозначения:
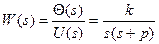 - передаточная функция электропривода;
- передаточная функция электропривода;
где Q(s) - угол поворота вала двигателя (выход объекта); U(s) - управляющий сигнал (вход объекта); р – динамический параметр объекта; s- переменная преобразования Лапласа; k- коэффициент усиления двигателя; W1(s)= kрпередаточная функция «П» регулятора в прямой цепи регулирования; W2(s) - передаточная функция измерительного устройства; W3(s)= kn× s = передаточная функция «ПД» регулятора в цепи обратной связи; R(s) – задание; Е(s) – ошибка в отработке задания.
Передаточная функция замкнутой системы равна:
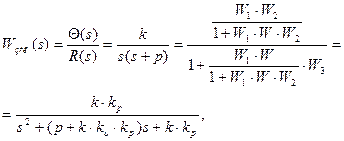
откуда имеем
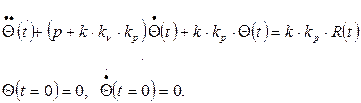 (4.1)
(4.1)
Переходная функция h(t) изображена на рис. 4.13. Из (4.1) получим коэффициент затухания колебаний:
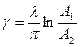 |
где l - частота затухающих колебаний, откуда g=g(kp,kn).
Полученные результаты показывают, что с увеличением коэффициентов усиления kp,kn увеличивается g. Это приводит к появлению нежелательных выбросов на выходе объектов управления. Кроме того, установившаяся ошибка в отработке задания не зависит от kp,kn: Е (t=¥)=R(t=¥)- h(t=¥)=0.
Замечание. Обычно передаточные функции W1,W3 реализуют в цифровом виде на контроллере, поэтому часто необходимо иметь цифровой аналог:
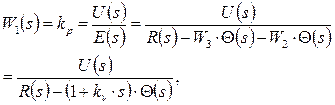
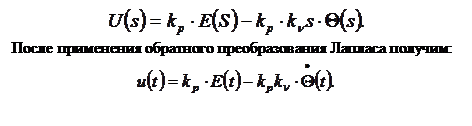 откуда
откуда
Положим 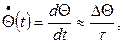

где t - шаг дискретизации по времени, тогда: 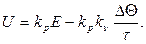
Это уравнение используется для представления ПД регулятора в виде программы контроллера.
Помимо структуры рис.4.12. для асинхронного электропривода используется ПД регулятор в форме последовательного корректирующего звена (структура 2, рис.4.14).
Из схемы следует:
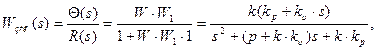
|
|
|
откуда имеем
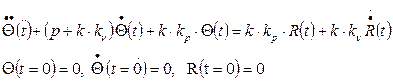 (4.2)
(4.2)
Сравнение (4.1) с (4.2) показывает, что при реализации структур рис.4.12. и структуры рис.4.14. будем иметь различные типы дифференциальных уравнений при описании замкнутой системы. Эти структуры имеют один общий недостаток: из-за отсутствия знаменателей в передаточных функциях регуляторов происходит усиление высокочастотных колебаний, которые поступают на вход объекта управления, и это может вызвать нежелательные последствия (перегрев, пробой изоляции и т.д.).
Для решения проблемы подавления высокочастотных колебаний рассматривается структура 3 (рис.4.15), в которой неизвестная передаточная функция регулятора выбирается из условия:
Wзам.3(s)=W зам.1(s), (4.3)
где Wзам.3(s)- передаточная функция замкнутой системы структуры 3, либо из условия:
Wзам.3(s)=W зам.2(s).
Найдем Wх(s) из условия (4.3)
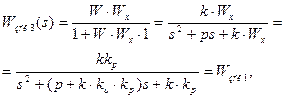
откуда имеем:
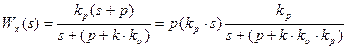
Таким образом Wх(s) представляет собой ПИД регулятор, который фильтрует высокочастотные колебания. Получим цифровой аналог ПИД-регулятора структуры 3 (рис.4.15). Из определения передаточной функции Wх(s) имеем:
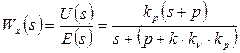 ,
,
откуда: kр (s + p) • E(s)=[ s + (p + k• kn k p)] • U(s).
В пространстве оригиналов этому уравнению соответствует дифференциальное уравнение:
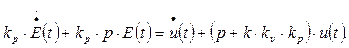
Аппроксимируем производные:
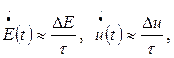
где DЕ=Е(t)-Е(t-t), Du=u(t)-u(t-t), тогда получим:
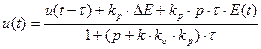
Это уравнение описывает ПИД регулятор в цифровой форме.
Структура 3 (рис.4.15) решает проблемы фильтрации высокочастотных колебаний, однако, при задании R(t)¹1(t) эта структура не обеспечивает сверхбыстрой его обработки. В этой связи структура 3 модифицируется в структуру 4 (рис.4.16), которая в своем составе имеет дополнительный блок, использующий нечеткие высказывания относительно зависимости G(E) (рис.4.17). Функции принадлежностей m(Е), m(G) изображены на рис. 4.18.
Динамические свойства системы с ПД регулятором улучшаются при использовании гибридного регулятора на базе нечетких высказываний. Для этого в качестве входной обратной связи обычного ПИД регулятора используется нечеткий регулятор, который настраивает коэффициент усиления G в зависимости от величины ошибки Е(t). При малой величине Е(t) в гибридном регуляторе используется величина G принятая для обычного ПИД регулятора, а при больших величинах Е(t) скорость коэффициента усиления G уменьшается. Сравнение обычного ПИД регулятора с гибридным с системе управления асинхронным электроприводом представлено на рис.4.19. Из него видно, что при управлении частотным преобразователем интеллектуальная управляющая стратегия на базе нечетких высказываний обладает преимуществом перед традиционным ПИД регулированием.
|
|
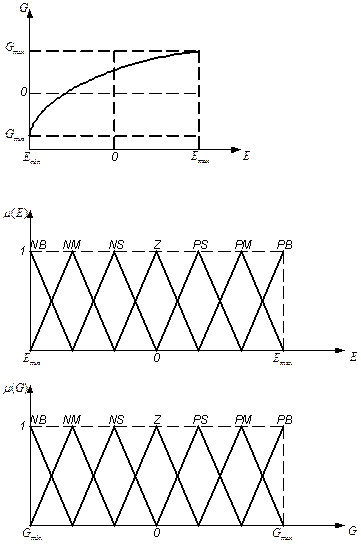
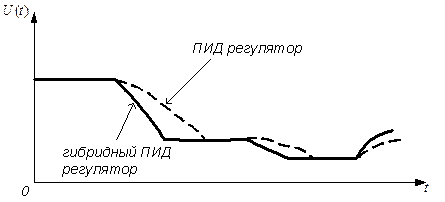 Рис.4.19 Изменение сигнала управления u(t) для ПИД и гибридного ПИД регулятора.
Рис.4.19 Изменение сигнала управления u(t) для ПИД и гибридного ПИД регулятора.
 2015-05-22
2015-05-22 3593
3593
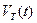 перемещения крана (т.
перемещения крана (т. 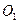 - начало разгона; т.
- начало разгона; т. 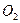 - конец разгона; т.
- конец разгона; т. 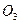 - начало торможения; т.
- начало торможения; т. 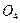 - конец торможения).
- конец торможения). 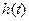 .
. 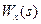 .
.