Нечеткие контроллеры

Алгоритм функционирования нечеткого контроллера (регулятора) описывается следующей системой уравнений:

R₁: А₁°r₁=A₁°(A₁₁®A₂₁)=B₁

R₂: А₂°r₂=A₂°(A₁₂®A₂₂)=B₂

{R_i}^К_i=1=:

R_K: А_K°r_K=A_K°(A_1K®A_2K)=B_K,

B=U^k_i=1B_i, z=dfz B,

где «°» композиция нечетких отношений, «®» – нечеткая импликация; 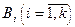локальный вывод из правила R_i;

В- общий вывод из базы правил {R_i}^К_i=1; 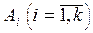=fuzz(x_i); A_jl= fuzz(x_j,x_l); fuzz- операция фазификации.

Эта система уравнений показывает, что в нечетком контроллере для получения его выхода z по входу х имеют место три взаимосвязанные стадии обработки информации (рис.3.15).

1. Преобразование входной физической переменной х в нечеткое множество – процедура фазификации (fuzz);

2. Логическая обработка нечетких переменных (композиция, импликация) базы правил контроллера, получение локальных и общего вывода базы правил в виде нечеткого множества В;

3. Преобразование нечеткого множества В в физическую переменную z – процедура дефазификации (dfz).

В соответствии со стадиями обработки информации алгоритм функционирования нечеткого контроллера по аналогии с классической теорией автоматического регулирования можно интерпретировать, как модель регулятора в терминах “вход-выход” в некотором новом пространстве, переход в которое из пространства оригиналов (физические переменные) осуществляется с помощью оператора “fuzz”. После проведения в новом пространстве (аналог пространства изображений в преобразовании Лапласа) некоторых операций, осуществляется обратное преобразование с помощью оператора dfz в исходное пространство. Сопоставление преобразований Фурье и Лапласа, принятых в классической теории автоматического регулирования, с преобразованием переменных типа “fuzz” и “dfz”, используемых в теории нечеткого управления, показано на рис.3.16. Подобная ситуация имеет место также в элементарной математике, когда такие относительно сложные операции как умножение и деление, путем логарифмического преобразования, могут быть заменены более простыми арифметическими операциями сложения и вычитания, и затем полученный результат с помощью обратного преобразования (антилогарифмирование) преобразуется в искомый результат.

Характерной особенностью преобразования информации в нечетком контроллере является то, что оператор “fuzz” не является единственным и определяется типом задания функций принадлежностей: треугольные, трапециидальные, колоколообразные и др. Логическая обработка нечетких множеств также не является единственной и определяется способами задания нечеткой импликации и композиции. Не единственным является оператор “dfz”: методы Сog, СОА и т.д.

Эту неединственность можно ассоциировать с тем фактом, что теория нечетких множеств появилась в результате попытки исчисления высказываний с неопределенными лингвистическими переменными: “большой”, “маленький”, “более или менее” и т.д., которыми обычно оперирует человек, и эти переменные в силу своей природы являются неоднозначными. В этой связи можно высказать предположение, что нечеткий контроллер является первым приближением в создании интеллектуальных систем управления, в которых сделана попытка формализации мыслительной деятельности человека и реализации этой деятельности в виде некоторого технического устройства. Архитектура нечеткого контроллера представлена на рис.3.17. Особенностью архитектуры является возможность параллельно обрабатывать правила базы правил, что позволяет существенно повышать быстродействие контроллера.

Преобразование переменных в Преобразование классической теории переменных в нечетком

автоматического регулирования контроллере

L L^-1