Евклидово пространство – это линейное пространство с некоторым образом введенной операцией «скалярного произведения».
1°. Определение и простейшие свойства.
Определение 1. Линейное пространство 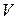 над полем вещественных чисел R называется евклидовым пространством E, если
над полем вещественных чисел R называется евклидовым пространством E, если 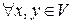 определено правило, ставящее им в соответствие вещественное число, называемое скалярным произведением
определено правило, ставящее им в соответствие вещественное число, называемое скалярным произведением 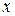 и
и 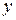 , обозначаемое
, обозначаемое 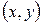 , и удовлетворяющее следующим аксиомам:
, и удовлетворяющее следующим аксиомам:
1) коммутативность: 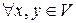 выполняется
выполняется 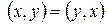 ;
;
2) дистрибутивность: 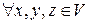 выполняется
выполняется 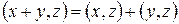 ;
;
3) 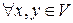 и
и 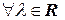 выполняется
выполняется 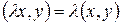 ;
;
4) 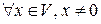 выполняется
выполняется 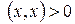 , причем
, причем 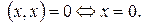
Примеры.
1) Множество геометрических векторов 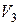 с обычным образом определенным скалярным произведением векторов (см. свойства скалярного произведения) образует евклидово пространство.
с обычным образом определенным скалярным произведением векторов (см. свойства скалярного произведения) образует евклидово пространство.
2) Множество 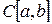 непрерывных на отрезке
непрерывных на отрезке 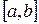 функций образует евклидово пространство, если скалярное произведение задается формулой:
функций образует евклидово пространство, если скалярное произведение задается формулой: 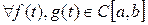
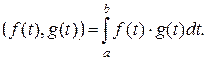
Свойство 1) скалярного произведения очевидно, 2) и 3) следуют из линейности интеграла, 4) следует из того, что 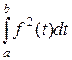 от неотрицательной функции неотрицателен и равен нулю только если
от неотрицательной функции неотрицателен и равен нулю только если 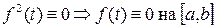 .
.
3) Пространство 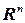 упорядоченных
упорядоченных 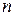 вещественных чисел образует евклидово пространство со скалярным произведением, задаваемым следующей формулой: если
вещественных чисел образует евклидово пространство со скалярным произведением, задаваемым следующей формулой: если 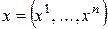 и
и 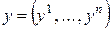 из
из 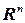 , то
, то
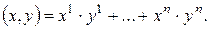 (1)
(1)
Свойство 1) − очевидно, свойства 2) и 3) следуют из определения сложения векторов в 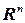 и умножения на число, т.е.
и умножения на число, т.е.
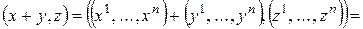
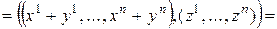
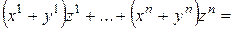
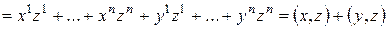 ;
;
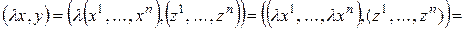
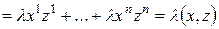 .
.
Свойство 4) следует из того, что 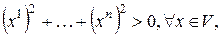 и равно нулю лишь тогда когда
и равно нулю лишь тогда когда 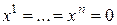 , т.е.
, т.е. 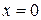 .
.
4) Пусть 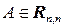 − матрица над
− матрица над 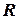 ипусть
ипусть 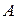 – симметричная, т.е.
– симметричная, т.е.  . Для любого
. Для любого 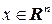 используем
используем 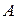 для построения квадратичной формы
для построения квадратичной формы 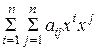 . Будем предполагать, что такая форма положительно определена, т.е.
. Будем предполагать, что такая форма положительно определена, т.е. 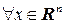 она больше нуля и равна нулю лишь если
она больше нуля и равна нулю лишь если 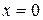 .
.
Такую матрицу 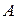 можно использовать для задания скалярного произведения в
можно использовать для задания скалярного произведения в 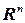 следующим образом:
следующим образом: 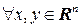 ,
,
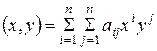 . (2)
. (2)
Свойство 1) следует из симметричности матрицы 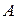 , 2) и 3) − из свойств вещественных чисел, 4) − из положительной определенности соответствующей квадратичной формы.
, 2) и 3) − из свойств вещественных чисел, 4) − из положительной определенности соответствующей квадратичной формы.
Замечание 1. Формула (1) Þ из (2) при 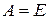 − единичная матрица.
− единичная матрица.
В общем виде скалярное произведение можно задать с помощью квадратичной формы, определенной в линейном пространстве. А именно, пусть 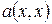 – положительно определенная квадратичная форма,
– положительно определенная квадратичная форма, 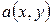 – её полярная форма. Тогда в силу свойств квадратичной формы имеем:
– её полярная форма. Тогда в силу свойств квадратичной формы имеем:
1°. 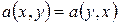 ;
;
2°. 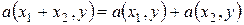 ;
;
3°. 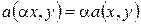 ;
;
4°. 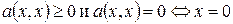 .
.
Как видно, эти аксиомы совпадают с аксиомами скалярного произведения Þ
Предложение 1. Скалярное произведение есть билинейная форма, соответствующая положительно определенной квадратичной форме, и любая такая форма может быть принята за скалярное произведение. Þ
Определение скалярного произведения может быть сформулировано как:
Определение 1'. Евклидовым пространством называется линейное пространство, в котором выбрана какая–либо фиксированная положительно определенная форма 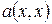 . Значение
. Значение 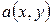 соответствующей ей билинейной формы считается при этом скалярным произведением векторов
соответствующей ей билинейной формы считается при этом скалярным произведением векторов 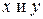 (оно ранее обозначалось как
(оно ранее обозначалось как 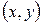 , а не
, а не 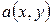 ).
).
Теорема 1 (неравенство Коши–Буняковского). Для любых элементов 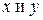 евклидового пространства
евклидового пространства 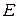 справедливо неравенство:
справедливо неравенство:
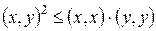 . (3)
. (3)
Неравенство (3) называется неравенством Коши–Буняковского.
Доказательство. По аксиоме 4) евклидова пространства 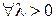 справедливо
справедливо
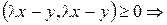
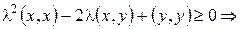
//так как квадратный трехчлен по 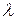 неотрицателен
неотрицателен 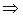 дискриминант
дискриминант 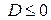 //
// 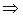
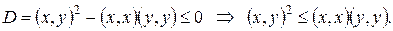 ■
■
Определение 2. Линейное пространство 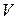 называется нормированным, если определено правило, по которому
называется нормированным, если определено правило, по которому 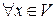 ставится в соответствие вещественное число, называемое нормой (или длиной) указанного элемента и обозначаемое
ставится в соответствие вещественное число, называемое нормой (или длиной) указанного элемента и обозначаемое 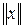 , удовлетворяющее следующим трем аксиомам:
, удовлетворяющее следующим трем аксиомам:
1) 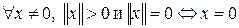 .
.
2) 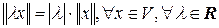 .
.
3) 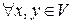 справедливо
справедливо 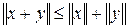 (неравенство треугольника или неравенство Минковского).
(неравенство треугольника или неравенство Минковского).
Теорема 2. Всякое евклидово пространство является нормированным, если в нем норму элемента 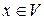 определить равенством
определить равенством
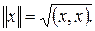
Доказательство. Проверим свойства нормированного пространства: аксиома 1) следует из 4) евклидова пространства, 2) следует из аксиом 1) и 3) евклидова пространства, 3) следует из неравенства Коши–Буняковского. Действительно,
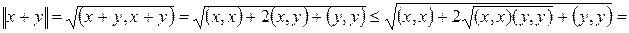
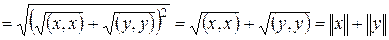 . ■
. ■
 2015-05-23
2015-05-23 5651
5651