Метод цепных подстановок (МЦП) используется для расчета влияния факторов во всех видах детерминированных факторных моделей: в аддитивных, мультипликативных, кратных и смешанных, то есть этот метод является универсальным. МЦП позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной подстановки в факторную модель вместо исходной величины каждого факторного показателя его текущего значения. С этой целью определяют ряд условных значений результативного показателя, которые учитывают изменение одного, затем двух, трех и так далее факторов. Сравнение величины результативного показателя до и после замены значения фактора позволяет исключить влияние всех факторов, кроме одного, и определить воздействие этого фактора на приращение результативного показателя. Методику использования метода цепных подстановок рассмотрим в общем виде на примере трехфакторной модели:
F = f (x, y, z).
Расчеты значений результирующего показателя при тех или иных значениях факторов будем нумеровать.
Первое действие – расчет значения результирующего показателя при исходных значениях всех факторов:
1) F 0 = f (x 0, y 0, z 0).
Во втором действии рассчитаем первое условное значение результирующего показателя (при текущем значении первого слева фактора и исходных значениях остальных факторов):
2) F усл 1 = f (x 1, y 0, z 0).
Исходное и первое условное значения результирующего показателя отличаются только за счет фактора х, соответственно, можно считать, что разница между этими значениями и есть приращение результирующего показателя под влиянием фактора х:
D Fx = F усл 1 – F 0.
В третьем действии по сравнению со вторым заменим с исходного на текущее значение следующего по цепочке (второго) фактора. Назовем рассчитанное таким образом значение результирующего показателя вторым условным значением:
3) F усл 2 = f (x 1, y 1, z 0).
Второе условное значение результирующего показателя отличается от первого условного значения только за счет фактора у, соответственно, разница между этими значениями и есть приращение результирующего показателя под влиянием фактора у:
D Fу = F усл 2 – F усл 1.
Нетрудно видеть, что при 4-м расчете замена очередного фактора приведет к тому, что в факторной модели все факторы будут в их текущем значении, соответственно, будет рассчитано текущее значение результирующего показателя:
4) F 1 = f (x 1, y1, z 1).
Текущее значение результирующего показателя отличается от второго условного значения только за счет фактора z, соответственно, можем рассчитать величину приращения результирующего показателя под влиянием фактора z как:
D Fz = F 1 – F усл 2.
После того, как рассчитаны оценки влияния на результирующий показатель всех факторов, нужно проверить, что это сделано правильно. Для этого суммируют все оценки, чтобы убедиться, что их сумма равна общей величине приращения результирующего показателя:
D Fx + D Fy + D Fz = D F = F 1 – F 0.
Если равенство выполняется, значит, оценки рассчитаны правильно. Запись суммы оценок влияния всех факторов позволяет не только выполнить проверку, но и наглядно представляет результаты решения прямой задачи. В такой записи видно, влияние каких факторов должно было привести к снижению уровня показателя, а каких – к увеличению; какие факторы оказали основное влияние на результирующий показатель, а какие – второстепенное.
Из формул метода цепных подстановок понятно, почему он так называется: замены значений факторов проводят последовательно, по цепочке. Влияние факторов с помощью МЦП рассчитывается одинаково для любых факторных моделей (аддитивных, мультипликативных, смешанных или кратных) с любым количеством факторов. Общий порядок замены факторов при расчетах – «слева направо» и «сверху вниз». Например, если факторная зависимость имеет вид:
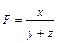 ,
,
то вначале нужно провести замену c исходного на текущее значение фактора x, затем – фактора y, и в последнюю очередь – замену z.
Применение метода цепных подстановок требует знания взаимосвязи факторов и умения правильно их классифицировать. При использовании МЦП в мультипликативных моделях и в смешанных моделях вида:
F = x (y ± z); F = xy + zw,
то есть в мультипликативно-аддитивных моделях, необходимо придерживаться следующей последовательности записи факторов в модель:
– на первое место (слева от знака умножения) следует ставить количественный, а затем – качественный факторный показатель;
– если не удается разделить факторы на количественные и качественные или если в мультипликативной модели несколько количественных и/или качественных факторов, то в каждой группе на первое место следует ставить фактор 1-го порядка (прямой), а затем – косвенный
(2-го и более высоких порядков);
– если предыдущих правил оказывается недостаточно, применяют еще одно: на первое место ставят обобщающий фактор, а затем – частный.
Применение перечисленных правил к мультипликативным и к смешанным мультипликативно-аддитивным моделям необходимо потому, что с арифметической точки зрения порядок факторов в этих моделях неважен (от перемены мест сомножителей результат не меняется), а вот результат факторного анализа от порядка факторов зависит. Иной порядок записи факторов в модель приводит к другим результатам решения прямой задачи, к другим оценкам влияния тех же отклонений факторов на результативный показатель. Например, если в факторной модели вида
1) F = x y z
записать факторы в другом порядке, например:
2) F = y z x,
а затем по одним и тем же данным оценить влияние факторов сначала по модели вида 1), а затем – по модели вида 2), оценки окажутся разными. Соблюдение определенного порядка записи факторов в модель позволяет получать единообразные результаты решения прямой задачи.
Покажем, как применять МЦП и интерпретировать результаты решения прямой задачи факторного анализа, на примерах.
Пример 1. Известно, что показатель F зависит от трех факторов: x, y и z – и является их произведением:
F = x y z.
Известны плановые и фактические значения факторов (см. табл. 5.2). Необходимо оценить, отличается ли фактическое значение F от планового, и если отличается, то оценить вклад каждого из факторов в это отклонение.
Таблица 5.2
 2015-05-25
2015-05-25 1822
1822
