Метод градиентного спуска

В природе мы нередко наблюдаем явления, сходные с решением задачи на нахождение минимума. К ним относится, в частности, стекание воды с берега котлована на дно. Упростим ситуацию, считая, что берега котлована унимодальные, т. е. они гладкие, а не содержат локальных углублений или выступов. Тогда вода устремится вниз в направлении наибольшей крутизны берега в каждой точке.

Переходя на математический язык, заключаем, что направление наискорейшего спуска соответствует направлению наибольшего убывания функции. Из курса математики известно, что направление наибольшего возрастания функции двух переменных 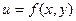характеризуется ее градиентом

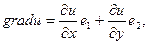
Где 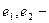единичные векторы (орты) в направлении координатных осей. Следовательно, направление, противоположное градиентному, укажет направление наибольшего убывания функции. Методы, основанные на выборе пути оптимизации с помощью градиента, называются градиентными. Идея метода градиентного спуска состоит в следующем. Выбираем некоторую начальную точку 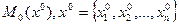, и вычисляем в ней градиент рассматриваемой функции. Делаем шаг в направлении, обратном градиентному:

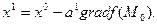
В результате приходим в точку 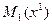, значение функции в которой обычно меньше первоначального 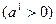. Если это условие не выполнено, т. е.значение функции не изменилось либо даже возросло, то нужно уменьшить шаг 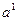. В новой точке процедуру повторяем: вычисляем градиент и снова делаем шаг в обратном к нему направлении:

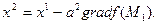
Процесс продолжается до получения наименьшего значения целевой функции. Строго говоря, момент окончания поиска наступит тогда, когда движение из полученной точки с любым шагом приводит к возрастанию значения целевой функции. Если минимум функции достигается внутри рассматриваемой области, то в этой точке градиент равен нулю, что также может служить сигналом об окончании процесса оптимизации. Приближенно момент окончания поиска можно определить аналогично тому, как это делается в других итерационных методах.

Формулы для частных производных можно получить в явном виде лишь в том случае, когда целевая функция задана аналитически. В противном случае эти производные вычисляются с помощью численного дифференцирования:

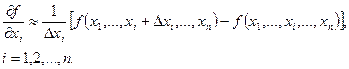
При использовании градиентного спуска в задачах оптимизации основной объем вычислений приходится обычно па вычисление градиента целевой функций в каждой точке траектории спуска. Поэтому целесообразно уменьшить количество таких точек без ущерба для самого решения. Это достигается в некоторых методах, являющихся модификациями градиентного спуска. Одним из них является метод наискорейшего спуска. Согласно этому методу, после определения в начальной точке направления, противоположного градиенту целевой функция, решают одномерную задачу оптимизации, минимизируя функцию вдоль этого направления. А именно, минимизируется функция

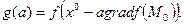
Для минимизации 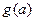можно использовать один из методов одномерной оптимизации. Можно и просто двигаться в направлении, противоположном градиенту, делая при этом не один шаг, а несколько шагов до тех пор, пока целевая функция не перестанет убывать. В найденной новой точке снова определяют направление спуска (с помощью градиента) и ищут новую точку минимума целевой функции и т. д. В этом методе спуск происходит гораздо более крупными шагами, и градиент функции вычисляется в меньшем числе точек.

Заметим, что сведение многомерной задачи оптимизации к последовательности одномерных задач на каждом шаге оптимизации рассмотрено в п.3.2 для метода покоординатного спуска. Разница состоит в том, что здесь направление одномерной оптимизации определяется градиентом целевой функции, тогда как покоординатный спуск проводится на каждом шаге вдоль одного из координатных направлений.