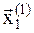1. Основные определения. Задачей многомерной оптимизации является минимизация функции U=f(x1,x2,...,xm) от m переменных (параметров) x1,x2,...,xm. Если нет ограничений на параметры x1,...,xm, то говорят о глобальной безусловной минимизации, если есть ограничения на параметры x1,...,xm, то говорят об условной минимизации.
Для сокращенного обозначения функции многих переменных удобно использовать векторное обозначение 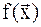 , при этом подразумевается, что каждой величине
, при этом подразумевается, что каждой величине 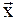 сопоставлен свой единственный набор значений величин x1,...,xm. В соответствии с этим величину
сопоставлен свой единственный набор значений величин x1,...,xm. В соответствии с этим величину 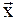 можно рассматривать как точку (элемент) m-мерного линейного пространства независимых переменных x1,...,xm. Если в этом пространстве ввести единичные векторы
можно рассматривать как точку (элемент) m-мерного линейного пространства независимых переменных x1,...,xm. Если в этом пространстве ввести единичные векторы 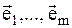 , поставленные в соответствие переменным x1,...,xm, то величину
, поставленные в соответствие переменным x1,...,xm, то величину 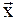 можно рассматривать как вектор:
можно рассматривать как вектор: 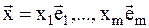 , а операции сложения и вычитания производить по правилу векторов.
, а операции сложения и вычитания производить по правилу векторов.
а) поверхность уровня. Множество точек 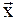 , для которых
, для которых 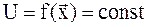 называется поверхностью уровня, для двух переменных это множество называется линей уровня
называется поверхностью уровня, для двух переменных это множество называется линей уровня
б) градиент. Вектор 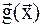 называется градиентом функции
называется градиентом функции 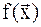 и обозначается:
и обозначается:
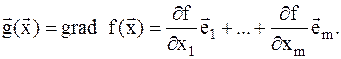 (8.1)
(8.1)
Вектор 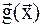 указывает направление наискорейшего возрастания функции, а вектор
указывает направление наискорейшего возрастания функции, а вектор 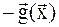 называется антиградиентом и указывает направление наискорейшего убывания функции. Градиент всегда перпендикулярен поверхности (линии) уровня.
называется антиградиентом и указывает направление наискорейшего убывания функции. Градиент всегда перпендикулярен поверхности (линии) уровня.
2. Необходимое и достаточное условия минимума функции многих переменных:
а) необходимое условие. Необходимым условием минимума функции многих переменных является условие равенства нулю ее градиента:
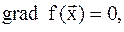 (8.2)
(8.2)
или
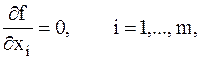
б) достаточное условие. Достаточным условием является условие положительной определенности матриц Гессе:
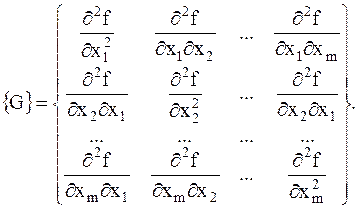 (8.3)
(8.3)
 Для положительной определенности матрица Гесса необходимо, чтобы ее собственные числа l1,...,lm были положительны. Собственные числа l1,...,lm являются корнями характеристического уравнения:
Для положительной определенности матрица Гесса необходимо, чтобы ее собственные числа l1,...,lm были положительны. Собственные числа l1,...,lm являются корнями характеристического уравнения:
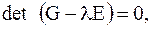 (8.4)
(8.4)
где det -определитель квадратной матрицы ранга m, Е - единичная матрица.
Матрица C=G-lE называется характеристической матрицей для матрицы G.
3. Основные методы безусловной многомерной минимизации:
а) покоординатный спуск. В методе покоординатного спуска
|
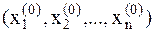 . Фиксируются все координаты кроме первой, и решается одномерная задача минимизации относительно переменной x1 (Рис.5). Затем фиксируются все координаты кроме второй, и опять решается задача одномерной минимизации относительно переменной x2 и т.д., т.е. поочередно производится спускание по всем координатам xi, до тех пор, пока не выполнятся все условия:
. Фиксируются все координаты кроме первой, и решается одномерная задача минимизации относительно переменной x1 (Рис.5). Затем фиксируются все координаты кроме второй, и опять решается задача одномерной минимизации относительно переменной x2 и т.д., т.е. поочередно производится спускание по всем координатам xi, до тех пор, пока не выполнятся все условия: 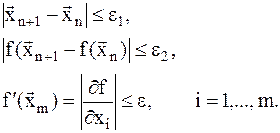 , (8.5)
, (8.5)
 Если линия уровня имеет изломы, что соответствует “оврагам” на поверхности
Если линия уровня имеет изломы, что соответствует “оврагам” на поверхности 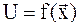 , то данный метод становится непригодным;
, то данный метод становится непригодным;
б) простой градиентный метод. В методе простого градиентного спуска выбирается начальная точка 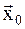 и начальное значение шага h. В точке
и начальное значение шага h. В точке 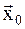 вычисляется градиент и делается шаг в направлении антиградиента (Рис.6):
вычисляется градиент и делается шаг в направлении антиградиента (Рис.6):
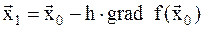 . (8.6)
. (8.6)
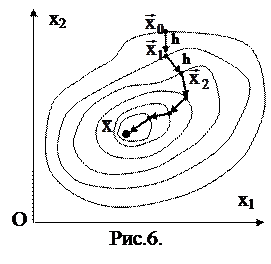 В результате вычисляется точка
В результате вычисляется точка 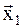 . Если выполняется условие
. Если выполняется условие 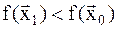 , то в точке
, то в точке 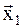 вычисляется градиент и делается шаг в направление антиградиента. Если условие
вычисляется градиент и делается шаг в направление антиградиента. Если условие 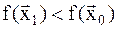 не выполняется, то шаг h уменьшают до тех пор, пока это условие не будет выполнено. Процесс продолжается до выполнения третьего условия (8.5).
не выполняется, то шаг h уменьшают до тех пор, пока это условие не будет выполнено. Процесс продолжается до выполнения третьего условия (8.5).
Недостатком метода является необходимость на каждом шаге вычислять значение градиента, что требует достаточно много времени;
в) метод наискорейшего спуска. Из начальной точки 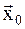 перпендикулярно линии уровня, т.е. в направлении антиградиента двигаются до тех пор, пока функция убывает, т.е. решают одномерную задачу минимизации для функции:
перпендикулярно линии уровня, т.е. в направлении антиградиента двигаются до тех пор, пока функция убывает, т.е. решают одномерную задачу минимизации для функции:
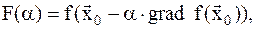 , (8.7)
, (8.7)
 где a выступает в качестве параметра.
где a выступает в качестве параметра.
В результате находится значение 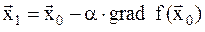 , соответствующее минимальному значению функции на выбранной прямой (Рис.7). Затем вычислительный процесс повторяется для точки
, соответствующее минимальному значению функции на выбранной прямой (Рис.7). Затем вычислительный процесс повторяется для точки 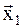 и т.д. Критерием окончания является третье условие (8.5);
и т.д. Критерием окончания является третье условие (8.5);
г) метод деформирован-ного многогранника. Когда 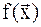 не является гладкой, и имеются множества точек, где она не дифференцируема, используются прямые методы. Наиболее известным из них является метод деформированного многогранника или метод Нелдера-Мида. Задается m+1 точка
не является гладкой, и имеются множества точек, где она не дифференцируема, используются прямые методы. Наиболее известным из них является метод деформированного многогранника или метод Нелдера-Мида. Задается m+1 точка 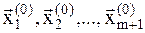 . При этом все разности
. При этом все разности 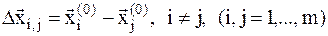 должны быть линейно независимыми.
должны быть линейно независимыми.
Обычно это делается следующим образом. Задаются координаты точки 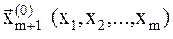 , а координаты остальных точек определяются с помощью соотношения:
, а координаты остальных точек определяются с помощью соотношения:
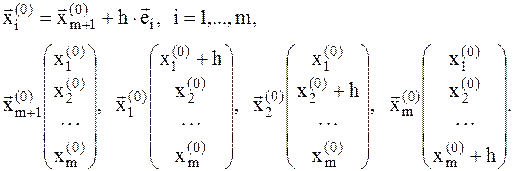 (8.8)
(8.8)
где h-параметр, который определяет стороны многогранника.
Точки 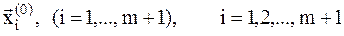 являются сторонами равнобедренного многогранника (на плоскости это треугольник).
являются сторонами равнобедренного многогранника (на плоскости это треугольник).
Исключается точка, в которой функция имеет самое большое значение, пусть это точка 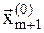 . Далее вычисляется среднее значение (или как иногда говорят центр тяжести) оставшихся точек:
. Далее вычисляется среднее значение (или как иногда говорят центр тяжести) оставшихся точек:
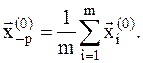 (8.9)
(8.9)
Далее вычисляется пробная точка:
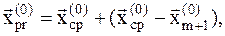 (8.10)
(8.10)
которая является симметричным отражением исключенной точки 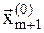 относительно точки
относительно точки 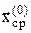 (Рис.8).
(Рис.8).
Вычисляется значение функции в пробной точке и сравнивается со значениями в всех исходных точках 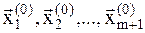 . Далее возможны варианты:
. Далее возможны варианты:
а) значение в пробной точке лежит между значениями исходных точек 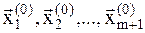 . Тогда исключенная точка
. Тогда исключенная точка 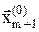 сразу заменяется на пробную точку
сразу заменяется на пробную точку 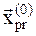 , и рассматривается новый многогранник с точками
, и рассматривается новый многогранник с точками 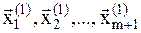 , где
, где 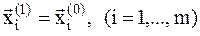 , а
, а 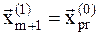 .
.
 |
б) значение в пробной точке
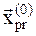 меньше чем в исключенной точке
меньше чем в исключенной точке 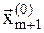 . Это значение также меньше, чем значение функции во всех остальных исходных точках
. Это значение также меньше, чем значение функции во всех остальных исходных точках 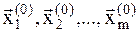 . Следовательно, мы удачно выбрали направление убывания функции и пробную точку переносим по этому направлению в два раза дальше, т.е. имеем новую пробную точку:
. Следовательно, мы удачно выбрали направление убывания функции и пробную точку переносим по этому направлению в два раза дальше, т.е. имеем новую пробную точку: 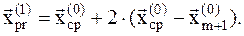 (8.11)
(8.11)
Вычисляем значение функции в новой пробной точке 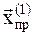 , и сравниваем со значением функции в начальной пробной точке
, и сравниваем со значением функции в начальной пробной точке 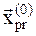 . Если значение в новой пробной точке
. Если значение в новой пробной точке 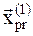 больше, чем в точке
больше, чем в точке 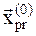 , то точка
, то точка 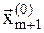 заменяется на первоначальную пробную точку
заменяется на первоначальную пробную точку 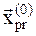 , и рассматривается новый многогранник с точками
, и рассматривается новый многогранник с точками 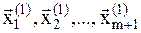 , где
, где 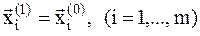 , а
, а 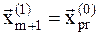 .
.
Если же значение в новой пробной точке меньше, чем в точке 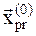 , то точка
, то точка 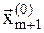 заменяется на новую пробную точку
заменяется на новую пробную точку 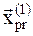 , и рассматривается новый многогранник с точками
, и рассматривается новый многогранник с точками 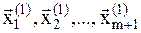 , где
, где 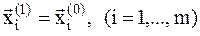 , а
, а 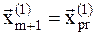 . Многогранник при этом деформируется.
. Многогранник при этом деформируется.
в) значение в пробной точке 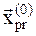 больше, чем в исключенной точке
больше, чем в исключенной точке 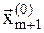 . Тогда выбирается новая пробная точка внутри многогранника:
. Тогда выбирается новая пробная точка внутри многогранника:
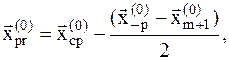 (8.12)
(8.12)
и тоже рассматривается новый многогранник с точками 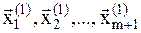 , где
, где 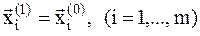 , а
, а 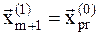 . Многогранник при этом также деформируется.
. Многогранник при этом также деформируется.
Периодически, после нескольких деформаций многогранника (обычно после 4-5 деформаций) многогранник восстанавливают. За новую базовую точку 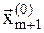 принимается точка, в которой функция минимальна, а величина шага h выбирается равной половине средней длине всех граней, исходящих из точки
принимается точка, в которой функция минимальна, а величина шага h выбирается равной половине средней длине всех граней, исходящих из точки 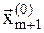 .
.
Процесс заканчивается, когда длины всех сторон многогранника, выходящих из точки с минимальным значением, станут меньше некоторого выбранного e или после очередного восстановления параметр h/2 станет меньше e.
Варианты задания №11
Найти точку минимума функции U(x,y) с точностью 0,1 указанным методом: а-покоординатный спуск, б-простой градиентный метод, в-метод наискорейшего спуска, г-метод деформированного многогранника.
1. 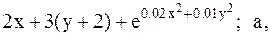 2.
2. 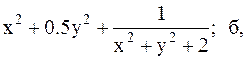
3. 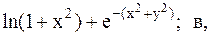 4.
4. 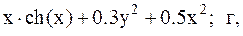
5. 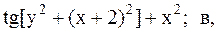 6.
6. 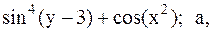
7. 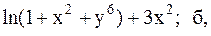 8.
8. 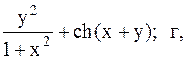
9. 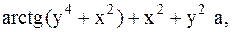 10.
10. 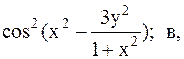
11. 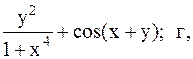 12.
12. 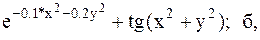
13. 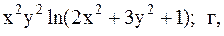 14.
14. 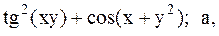
15. 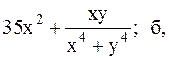 16.
16. 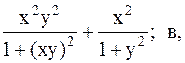
17. 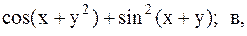 18.
18. 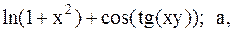
19. 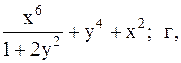 20.
20. 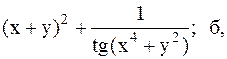
21. 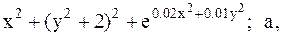 22.
22. 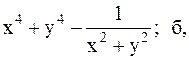
23. 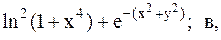 24.
24. 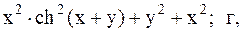
25. 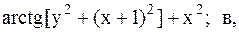 26.
26. 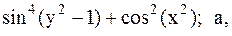
27. 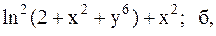 28.
28. 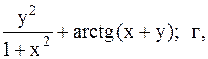
29. 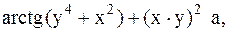 30.
30. 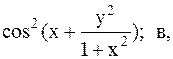
31. 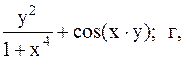 32.
32. 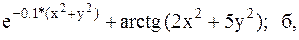
33. 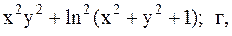 34.
34. 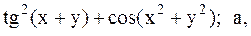
35. 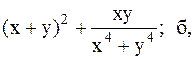 36.
36. 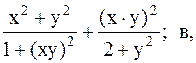
37. 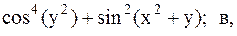 38.
38. 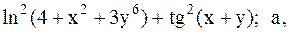
39. 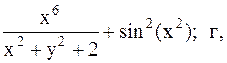 40.
40. 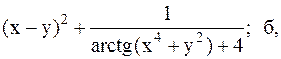
 2015-03-22
2015-03-22 6147
6147