Бинарное отношение обладающее свойствами рефлективности, симметричности и транзитивности называется эквивалентным.
Отношение эквивалентности разбивает множество М на два подмножества, эквивалентных между собой элементов 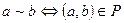
Подмножество эквивалентных элементов называется классами эквивалентности. Классы эквивалентности на множестве М образуют дизъюнктивную сумму.
Пример: Пусть множество М – множество всех прямых на плоскости. Будет ли эквивалентное соотношение?
а) параллельности прямых
б) перпендикулярности прямых
а) Проверим выполнение свойств:
1. рефлективность а 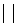 а – выполняется
а – выполняется
2. транзитивность, а 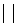 в, в
в, в 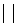 с
с 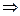 а
а 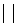 с – выполняется
с – выполняется
3. симметричность, а 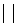 в,
в, 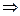 в
в 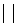 а – выполняется
а – выполняется
следовательно параллельность прямых - эквивалентное соотношение.
б) 1. рефлективность а 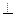 а – не выполняется
а – не выполняется
2. транзитивность, а 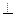 в, в
в, в 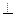 с
с 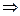 а
а 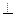 с – не выполняется
с – не выполняется
3. симметричность, а 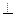 в,
в, 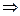 в
в 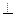 а – выполняется
а – выполняется
Отношение получается антирефлексивное, не транзитивное, симметричное.
 2015-06-04
2015-06-04 1305
1305
