Непериодическую функцию можно представить как периодическую с периодом 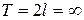 . При
. При 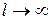 числа
числа 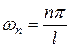 будут охватывать все значения, то есть спектр волновых чисел будет непрерывным, и суммирование в ряде Фурье (34) заменится на интегрирование.
будут охватывать все значения, то есть спектр волновых чисел будет непрерывным, и суммирование в ряде Фурье (34) заменится на интегрирование.
Если непериодическая функция f(t) удовлетворяет условиям Дирихле на любом конечном интервале и 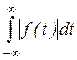 сходится, то ее можно представить интегралом Фурье, который в комплексной форме имеет вид
сходится, то ее можно представить интегралом Фурье, который в комплексной форме имеет вид
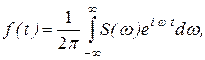 (35)
(35)
где S(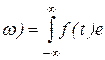
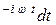 . (36)
. (36)
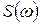 является аналогом коэффициента
является аналогом коэффициента 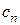 (формулы 34 и 36). Однако, если
(формулы 34 и 36). Однако, если 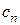 характеризует амплитуду волнового числа
характеризует амплитуду волнового числа 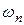 , то
, то 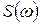 - плотность распределения комплексной амплитуды. Поэтому данную функцию называют спектральной плотностью или спектральной функцией. Ее модуль
- плотность распределения комплексной амплитуды. Поэтому данную функцию называют спектральной плотностью или спектральной функцией. Ее модуль 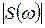 называют амплитудой спектральной плотности или амплитудным спектром.
называют амплитудой спектральной плотности или амплитудным спектром.
Формулу (36) называют прямым преобразованием Фурье, а формулу (35) - обратным. Вместе они составляют пару преобразований Фурье.
В точках разрыва функции интеграл Фурье как и сумма ряда Фурье равен полусумме пределов функции слева и справа.
Интеграл Фурье можно представить аналогично формулам (24-25), то есть без комплексных выражений
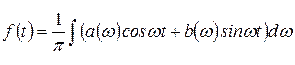 ,
,
где 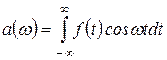 ,
, 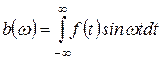 .
.
Спектральная плотность 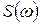 выражается через функции
выражается через функции 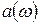 и
и 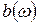 следующим образом
следующим образом
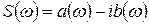 . (38)
. (38)
Пример 34. Найти спектр прямоугольного импульса.
Прямоугольный импульс (рис.5) высотой 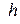 и длительностью t задан уравнениями:
и длительностью t задан уравнениями:
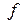
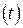 =
= 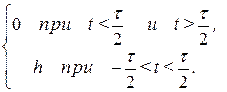
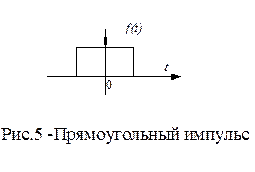
По формуле:
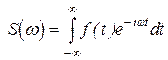 , находим спектральную плотность.
, находим спектральную плотность.
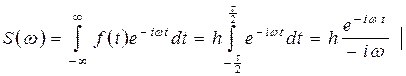
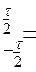
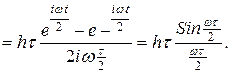
Так как 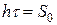 - площадь импульса, то
- площадь импульса, то 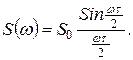
ВОПРОСЫ И УПРАЖНЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Что называется числовым рядом, частичной суммой, общим членом ряда, его суммой?
2. Запишите ряд в кратком виде. После записи проверьте, получаются ли из них все члены ряда:
а) 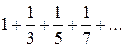 ;
;
б) 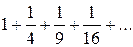 .
.
3. Сформулируйте необходимый признак сходимости ряда. Используя его, докажите расходимость рядов:
а) 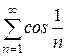 ; б)
; б) 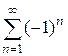 ; в)
; в) 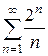 .
.
4. Сформулируйте достаточные признаки сходимости рядов с положительными членами: признак Даламбера, признаки Коши. Исследуйте на сходимость ряды:
а) 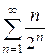 . Ответ: ряд сходится.
. Ответ: ряд сходится.
б) 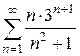 . Ответ: ряд расходится.
. Ответ: ряд расходится.
в) 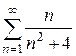 . Ответ: ряд расходится.
. Ответ: ряд расходится.
5. Сформулируйте признак Лейбница сходимости знакочередующихся рядов.
6. Дайте определение абсолютно и условно сходящихся рядов.
7. Что называется областью сходимости функционального ряда?
8. Выведите формулу для вычисления радиуса сходимости степенного ряда?
9. Как исследуется сходимость степенного ряда в граничных точках области сходимости?
10. Найти области сходимости следующих рядов:
а) 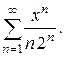 Ответ.
Ответ. 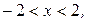 при x =-2
при x =-2
ряд сходится условно.
б) 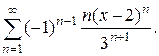 Ответ.
Ответ. 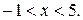
в) 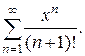 Ответ.
Ответ. 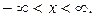
11.Разложить в ряд по степеням x следующие функции:
а) 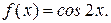 Ответ.
Ответ. 
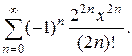
б) 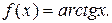 Ответ.
Ответ. 
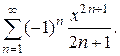
в) 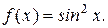 Ответ.
Ответ. 
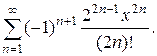
Указание. Использовать формулу 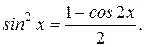
12. Вычислить приближенно 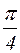 , воспользовавшись рядом
, воспользовавшись рядом
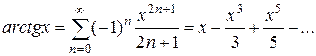
и взяв сумму первых пяти членов при х= 1. Какова будет величина допущенной ошибки?
13. Разложить функцию в ряд Фурье
а) 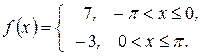
б) 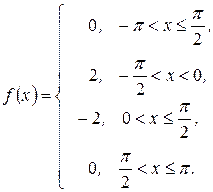
Ответ: а) 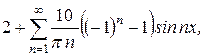 б)
б) 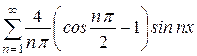 .
.
14. Разложить функцию в ряд Фурье по косинусам, продолжив ее в симметричный интервал:
а) 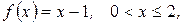 Ответ:.
Ответ:. 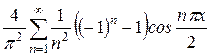 .
.
б) 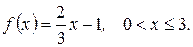 Ответ:
Ответ: 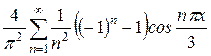 .
.
15. Написать формулу прямого и обратного преобразований Фурье.
16. Что называется спектральной плотностью?
17. Найти комплексный и амплитудный спектр функции
 Ответ:
Ответ: 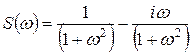 ,
,
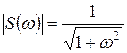 .
.
КОНТРОЛЬНАЯ РАБОТА № 4.
Исследовать знакоположительные числовые ряды (а) на сходимость и знакочередующиеся числовые ряды (б) на абсолютную и условную сходимость.
1. а) 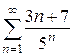 ; б)
; б) 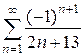 .
.
2. а) 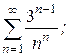 . б)
. б) 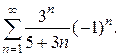
3. а) 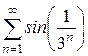 ; б)
; б) 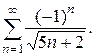 .
.
4. а) 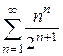 ; б)
; б) 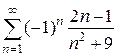 .
.
5. а) 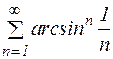 ; б)
; б) 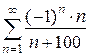 .
.
6. а) 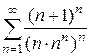 ; б)
; б) 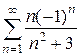 .
.
7. а) 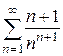 ; б)
; б) 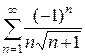 .
.
8. а) 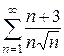 ; б)
; б) 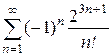 .
.
9. а) 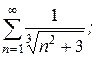 б)
б) 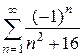 .
.
10 а)  ; б)
; б) 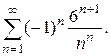
Найти интервал сходимости степенного ряда и выяснить вопрос о сходимости ряда на концах интервала.
Таблица 1.
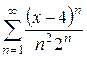
| 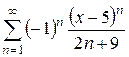
| ||
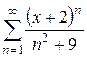
| 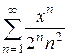
| ||
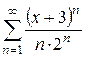
| 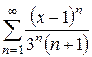
| ||
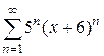
| 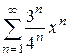
| ||
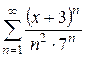
| 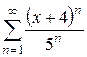
|
Разлагая подынтегральную функцию в ряд, вычислить приближенно значение определенного интеграла 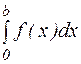 с точностью до e=0,001.
с точностью до e=0,001.

 Таблица 2.
Таблица 2.
| № | 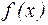
| b | № | 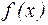
| b |
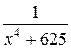
| 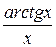
| 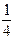
| |||
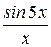
| 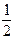
| 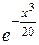
| |||
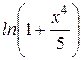
|
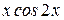
|
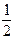
| |||
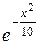
| 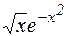
| ||||
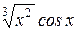
| 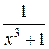
| 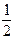
|
Разложите в ряд Фурье периодическую функцию, аналитическое выражение которой задано на промежутке длиной, равной периоду.
31. 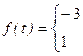
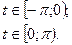 32.
32. 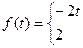
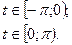
33. 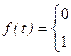
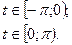 34.
34. 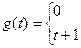
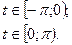
35. 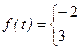
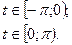 36.
36. 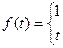
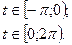
37. 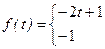
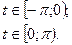 38.
38. 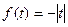 ,
, 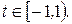
39. 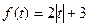
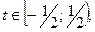 Т=1. 40.
Т=1. 40. 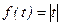 ,
, 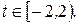


Разложите функцию 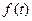 в ряд Фурье по синусам. Постройте график суммы ряда.
в ряд Фурье по синусам. Постройте график суммы ряда.
41. 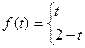
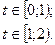 42.
42. 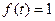
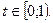
43. 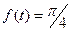
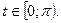 44.
44. 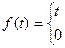
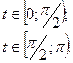
45. 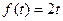
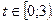 46.
46. 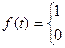
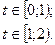
47. 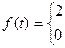
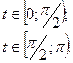 48.
48. 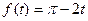
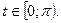
49. 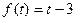
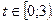 50.
50. 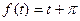
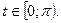
Найдите преобразование Фурье функции 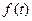 .
.
51. 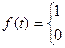
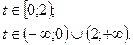 52.
52. 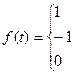
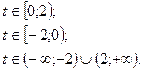
53. 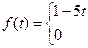
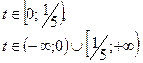 54.
54. 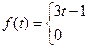
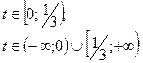
55. 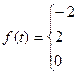
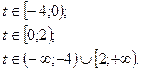 56.
56. 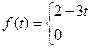
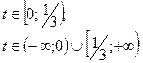
57. 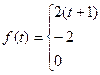
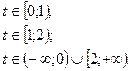 58.
58. 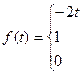
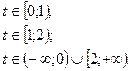
59. 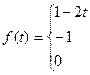
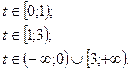 60.
60. 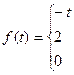
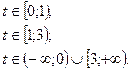
С О Д Е Р Ж А Н И Е
| Введение Рабочая программа Варианты контрольных заданий Литература Числовые ряды Числовой ряд. Общий член ряда Сходящиеся и расходящиеся ряды Основные свойства сходящихся рядов Признаки сходимости числовых рядов Необходимый признак сходимости ряда Достаточные признаки сходимости знакоположительных рядов Знакочередующиеся и знакопеременные ряды Знакочередующиеся ряды Знакопеременные ряды Функциональные ряды Функциональный ряд и его область сходимости Степенные ряды Ряды Маклорена и Тейлора Ряды Фурье Ряд Фурье в комплексной форме Интеграл Фурье Вопросы и упражнения для самопроверки Контрольная работа №4 |
План 2001/2002, поз. 31
ГладковЛев Львович
Гладкова Галина Александровна
Методические указания и контрольные задания по дисциплине «Высшая математика», часть IV для студентов уровня ВО заочной формы обучения специальности 145. 01. 03 «Сети телекоммуникаций»
Редактор Вердыш Н.В.
Подписано к печати 20.12.2002
Формат 60S84/16
Усл. Печ. Л. 2,3. Уч. - изд. Л. 2,0
Тираж 90 экз. Заказ 675.
Высший государственный колледж связи
220114 г. Минск, Староборисовский тракт 8, к. 2.
 2015-06-05
2015-06-05 389
389







