Пусть две прямые p 1 и p 2 в пространстве заданы своими каноническими уравнениями:
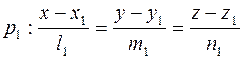 ,
,
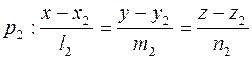 .
.
Параллельность, перпендикулярность и угол между прямыми вполне определяется их направляющими векторами 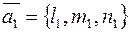 и
и 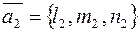 .
.
Условие параллельности:
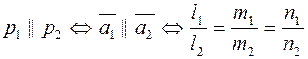 .
.
Условие перпендикулярности:
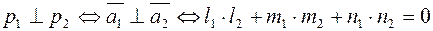 .
.
Угол φ между прямыми определяется по формуле:
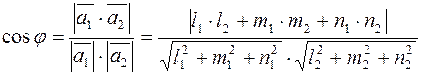 .
.
Две прямые в пространстве могут: 1) пересекаться; 2) быть параллельными; 3) скрещиваться. В первых двух случаях прямые лежат в одной плоскости. Наряду с направляющими векторами прямых 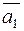 и
и 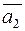 , рассмотрим вектор
, рассмотрим вектор 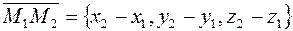 , где
, где 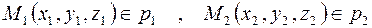 . Прямые лежат в одной плоскости тогда и только тогда, когда эти векторы компланарны, что, в свою очередь, равносильно равенству нулю их смешанного произведения. Выразив смешанное произведение через проекции векторов, получим условие принадлежности прямых p 1 и p 2 одной плоскости:
. Прямые лежат в одной плоскости тогда и только тогда, когда эти векторы компланарны, что, в свою очередь, равносильно равенству нулю их смешанного произведения. Выразив смешанное произведение через проекции векторов, получим условие принадлежности прямых p 1 и p 2 одной плоскости:
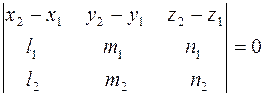 .
.
 2015-06-28
2015-06-28 723
723








