2015-06-28
2706
Определение. Всякий ненулевой вектор, лежащий на данной прямой или параллельный ей, называется ее направляющим вектором. Обозначение: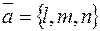 
.
Составим уравнение прямой, проходящей через точку M 0(x 0, y 0, z 0) в направлении вектора 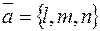. Возьмем текущую точку прямой M (x, y, z) и рассмотрим вектор 
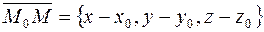. Он лежит на данной прямой и поэтому коллинеарен ее направляющему вектору 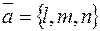. Осталось написать условие коллинеарности, т.е. пропорциональность проекций:
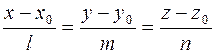. (2)
Это и есть канонические уравнения прямой, проходящей через точку M 0(x 0, y 0, z 0) и имеющей направляющий вектор .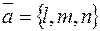
Пример. Найти канонические уравнения прямой
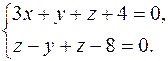(3)
Решение. Чтобы составить канонические уравнения прямой, нужно: 1) найти какую-либо точку прямой; 2) найти направляющий вектор прямой.
1) Найти какую-нибудь точку прямой (3) – это означает найти какое-нибудь решение этой системы двух уравнений с тремя неизвестными. Положим, например, x= 0. Система (3) превратится в
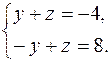
Отсюда нетрудно найти: z=2, y= –6. Итак, точка M 0(0;–6; 2) принадлежит прямой (3).
2) Прямая определена как пересечения двух плоскостей, значит она лежит в каждой из них и поэтому перпендикулярна их нормальным векторам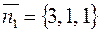 
и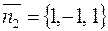 
. В качестве направляющего вектора можно взять любой вектор перпендикулярный к векторам 
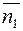и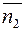 
, например, их векторное произведение
|
|
|
,
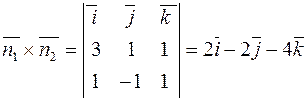или вектор, коллинеарный ему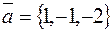 
. Итак, искомые канонические уравнения имеют вид
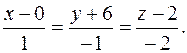
Пример. Составить уравнения прямой, проходящей через точки M 1(x 1, y 1, z 1)и M 2(x 2, y 2, z 2).
Решение. Для того, чтобы использовать канонические уравнения (2), положим M 0 =M 1,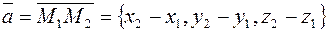 
. Получим:
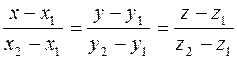. (4)
Имея эти уравнения, предыдущей пример можно решить, не находя направляющий вектор прямой. Надо только найти не одну точку, лежащую на прямой, а две.
