Плоскость в пространстве

Лемма

Преобразование системы координат не меняет степень уравнения алгебраической поверхности.

Без д-ва

Теорема 4

Любое уравнение первой степени от трех неизвестных описывает плоскость в пространстве. Любая плоскость в пространстве описывается некоторым уравнением первой степени.

Доказательство:

1. Рассмотрим уравнение:

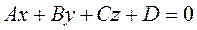(33)

Пусть уравнение (33) описывает поверхность .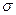

Пусть 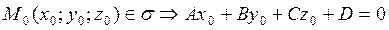. Вычтем из (33) данное уравнение:

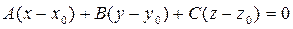(34).

Пусть вектор 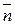имеет координаты 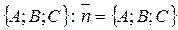. Из (34) 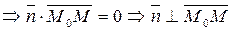(данное расположение возможно, когда M “бегает” по плоскости) 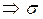- плоскость.

2. Пусть 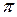- плоскость.

Введем систему координат, в которой плоскость 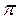совпадает с плоскостью 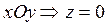(в силу определения уравнения поверхности). Это уравнение первой степени. В силу леммы плоскость 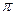будет иметь уравнение первой степени в любой другой системе координат.

Теорема доказана

Определение

Уравнение (33) называется общим уравнением плоскости в пространстве.

Определение

Вектор 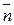называется нормальным вектором плоскости с уравнением (33) и (34).