II способ построения уравнения плоскости

Задача:

1. Дано: , ,

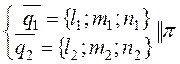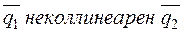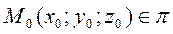
Найти: уравнение плоскости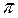

Решение:

Пусть 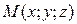- текущая точка на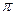

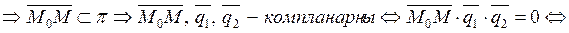
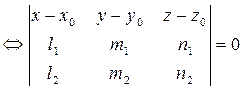(36) - уравнение плоскости, проходящей через точку M ₀ пареллельно векторам 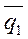и .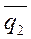

Решим эту задачу иначе.

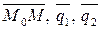- компланарны, 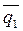и 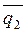- линейно независимы, поэтому могут быть взяты в качестве базиса на плоскости 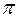. Приложим эти векторы к точке M ₀. Любой вектор этой плоскости может быть разложен по векторам 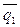и 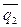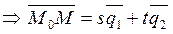. Запишем последнее равенство в координатах:

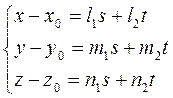
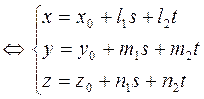(37) – параметрические уравнения плоскости.

II способ основан на условии компланарности трех векторов 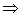смешанное произведение равно 0.

2. Дано: 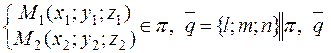не коллинеарен .

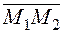Найти: уравнение плоскости .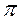

Решение:

Сведем задачу к задаче 1):

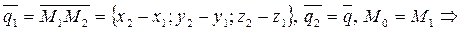используем готовый способ решения задачи 1).

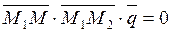
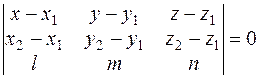(38) – уравнение плоскости, проходящей через две данные точки, параллельно данному вектору.

3. Дано: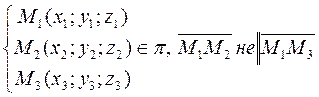

Найти: уравнение плоскости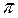

Решение:

Приводим задачу к задаче 1):

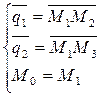
Решаем аналогично.

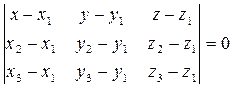(39) - уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.