Нормированное уравнение плоскости. Расстояние от точки до плоскости

Пусть дана плоскость 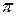, не проходящая через начало координат.

P – основание перпендикуляра, опущенного из начала координат на плоскость .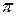

Пусть 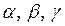- углы, составленные вектором 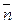с осями координат.

,

.

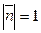
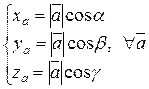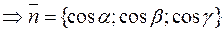Рассмотрим произвольную точку M (x; y; z) на плоскости .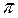

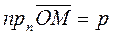, т.к. 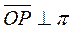(проекция произвольной точки M на 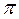на ось, перпендикулярную 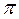, совпадает с p).

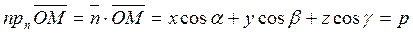
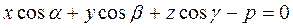(43) - нормальное или нормированное уравнение плоскости.

Переход от общего уравнения плоскости к нормированному виду

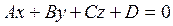
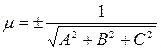– нормирующий множитель. Умножим на него обе части общего уравнения плоскости.

Знак 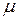выбираем противоположным знаку D.