Взаимное расположение прямых

Прямые в пространстве могут пересекаться, быть параллельными или скрещиваться.

Пусть прямые 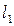и 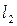заданы своими каноническими уравнениями:

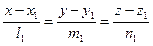
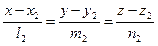
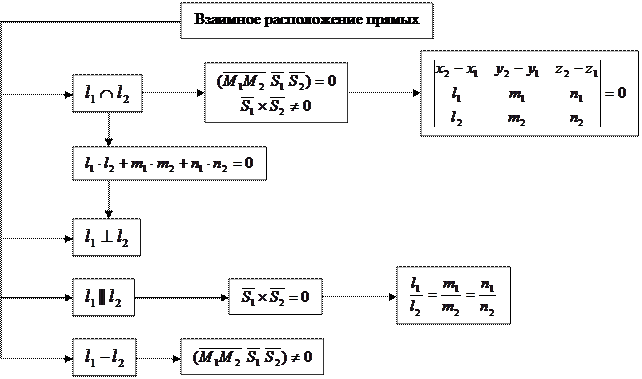Структурная схема 3

Замечание По схеме 4 устанавливается взаимное расположение прямых в пространстве.

Задача 22 Доказать, что прямые, заданные уравнениями: ;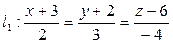

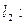
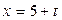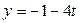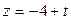, , , пересекаются.

Решение

Рассмотрим 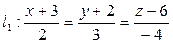, тогда , ;

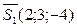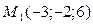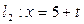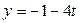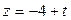, , , тогда , .

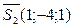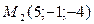1 Найдём смешанное произведение векторов , ,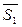

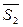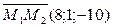
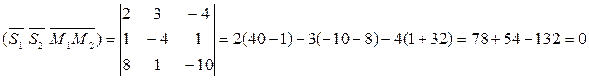
Смешанное произведение равно 0, значит вектора 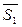, , 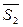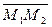компланарны, т.е. лежат в одной плоскости.

Найдём векторное произведение , :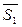

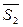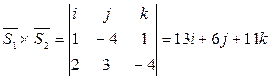
Имеем: 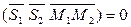, , 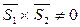значит 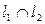(Схема 4)

Раздел 3 Дополнительные уравнения плоскости