АЛГОРИТМ 6 Уравнение плоскости, проходящей через две параллельные прямые Дано: 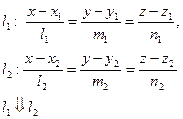 ________________________________ Составить уравнение плоскости α: ________________________________ Составить уравнение плоскости α: 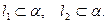 Решение Выполним схематичный чертеж (рис.22) Решение Выполним схематичный чертеж (рис.22)  Рис. 22 1 Выберем одну из точек Рис. 22 1 Выберем одну из точек 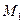 или или 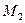 , через которые проходят прямые , через которые проходят прямые 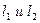 , и которые лежат в плоскости α. Возьмем точку , и которые лежат в плоскости α. Возьмем точку 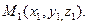 2 Найдем нормальный вектор плоскости 2 Найдем нормальный вектор плоскости 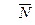 . . 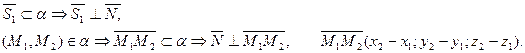 Тогда имеем: Тогда имеем: 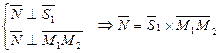 . . 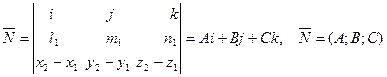 . 3 Подставим координаты точки . 3 Подставим координаты точки 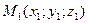 и вектора и вектора 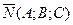 в «основное» уравнение (1) плоскости, получим в «основное» уравнение (1) плоскости, получим 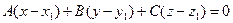 |
Задача 24 Доказать, что прямые 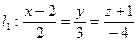 и
и 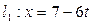 ,
, 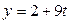 ,
, 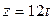 параллельны, и составить уравнение плоскости
параллельны, и составить уравнение плоскости 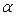 , проходящей через данные прямые.
, проходящей через данные прямые.
Решение
1 Рассмотрим направляющие векторы прямых 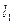 ,
, 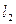 :
:
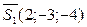 ,
, 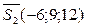
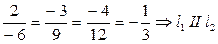
2 Выберем одну из точек 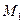 или
или 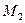 , через которые проходят прямые
, через которые проходят прямые 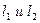 , и которые лежат в плоскости α.
, и которые лежат в плоскости α.
Возьмем точку 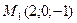 (рис.28)
(рис.28)
3 Найдем нормальный вектор плоскости 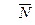 .
.
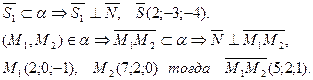
Тогда имеем: 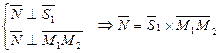 .
.
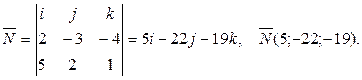
3 Подставим координаты точки 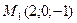 и вектора
и вектора 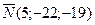 в уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
в уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору 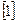 , получим
, получим
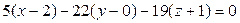 ,
,
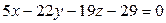 .
.
Ответ: 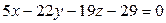
 2015-06-28
2015-06-28 12734
12734
