1. Векторы в пространстве. В пространстве, как и на плоскости, вектором называется направленный отрезок. Векторы, расположенные на прямых, параллельных одной и той же плоскости, или лежащие в этой плоскости, называются компланарными.
Три вектора, среди которых имеется хотя бы один нулевой вектор, считаются компланарными.
Любой вектор 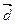 пространства можно разложить по трем заданным некомпланарным векторам
пространства можно разложить по трем заданным некомпланарным векторам 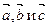 :
:
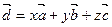
2. Прямоугольная система координат в пространстве. Пусть в пространстве задана тройка попарно перпендикулярных единичных векторов 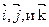 , отложенных от некоторого начала — точки О. Такую тройку векторов называют прямоугольным базисом в пространстве. Совокупность начала О и прямоугольного базиса
, отложенных от некоторого начала — точки О. Такую тройку векторов называют прямоугольным базисом в пространстве. Совокупность начала О и прямоугольного базиса 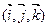 называют прямоугольной системой координат в пространстве.
называют прямоугольной системой координат в пространстве.
Разложение вектора 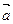 в базисе
в базисе 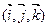 имеет вид
имеет вид
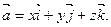
Если началом вектора 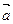 является точка
является точка 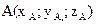 концом — точка
концом — точка 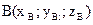 , то вектор
, то вектор 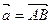 имеет координаты, равные разностям соответствующих координат точек B и A:
имеет координаты, равные разностям соответствующих координат точек B и A:
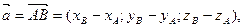
и записывается в виде
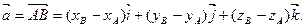
3. Правила действий над векторами, заданными своими координатами.
Если в базисе 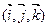 заданы векторы
заданы векторы 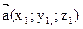 и
и 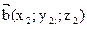 , то:
, то: 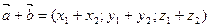 ;
;
координаты разности двух векторов равны:
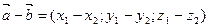 ;
;
координаты произведения вектора на число: 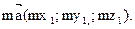
4. Условие коллинеарности двух векторов. Условие коллинеарности двух векторов 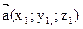 и
и 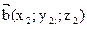 имеет вид
имеет вид
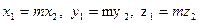
Если 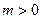 , то векторы
, то векторы 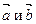 имеют одинаковое направление; если т<0, то направления векторов противоположны.
имеют одинаковое направление; если т<0, то направления векторов противоположны.
5. Длина вектора. Длина вектора 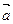 (расстояние между двумя точками) вычисляется по формуле
(расстояние между двумя точками) вычисляется по формуле
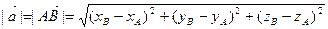
Длина радиус-вектора 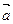 вычисляется по формуле
вычисляется по формуле
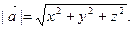
6. Деление отрезка в данном отношении. Если отрезок АВ разделен точкой С в отношении 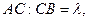 , то координаты точки С находятся по формулам
, то координаты точки С находятся по формулам
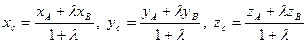
При 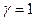 получаются формулы для нахождения координат середины отрезка:
получаются формулы для нахождения координат середины отрезка:
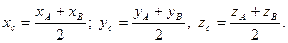
7. Направляющие косинусы вектора. Углы, образуемые радиус-вектором 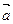 с координатными осями Ox, Оу, Oz, вычисляются по формулам
с координатными осями Ox, Оу, Oz, вычисляются по формулам
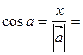
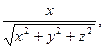
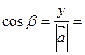
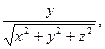
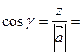
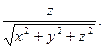
Косинусы углов, вычисляемые по этим формулам, называются направляющими косинусами вектора 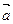 .
.
Для направляющих косинусов вектора имеет место соотношение
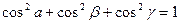 .
.
 2015-06-28
2015-06-28 1836
1836
