Теорема (о мощности прямого произведения множеств)

Пусть 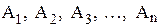- конечные множества и

.

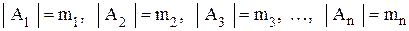Тогда мощность множества 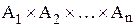равна произведению мощностей множеств :

.

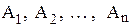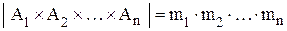Доказательство:

Докажем методом математической индукции. Для n = 1. Теорема тривиально верна. Предположим, что она верна для n = k. Докажем, что она справедлива для n = k + 1.

По предположению

.

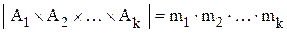Возьмем любой вектор из 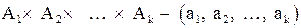и припишем справа элемент 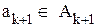, так как 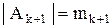, то это можно сделать 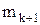способом. При этом мы получим 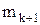различных векторов из 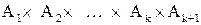лишь из одного вектора 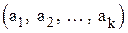из 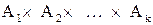. Так как таких векторов в 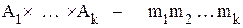штук, то приписыванием к каждому из них справа всех по очереди элементов из 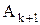получим 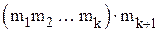новых векторов из 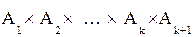, причем все они различны и других векторов в 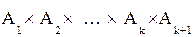не содержится. Поэтому для n = k + 1 теорема верна и верна для любых n.

Следствие: .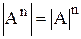

Эта теорема и ее следствие лежат в основе очень многих комбинаторных фактов.