Векторы

Определение: Вектор - это упорядоченный набор элементов (“кортеж” - размещение).

Определение: Координаты или компоненты вектора - это элементы, образующие вектор. Координаты нумеруются слева направо.

Определение: Длина (размерность) вектора - число координат вектора.

В отличие от элементов множества, его координаты могут совпадать. Обозначение вектора: в круглых скобках, координаты - через запятую (0, 5, 4, 5, 0, 1). Иногда скобки и даже запятые опускаются.

Определение: Векторы длины 2 называют упорядоченными парами;

длины 3 - тройками;

длины 4 - четверками;

длины n - n-ками.

Определение: Два вектора равны, если они имеют одинаковую длину, и соответствующие их координаты равны, т. е.

,

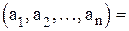
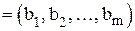если m = n и

.

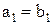
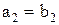
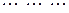
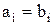
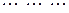
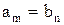Определение: Прямым произведением множеств А и В (обозначается А 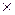В) называется множество всех пар (a, b) таких, что 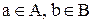. В частности, если А = В, то обе координаты принадлежат А (обозначим ).

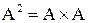Аналогично:

Определение: Прямое произведение n множеств 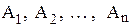(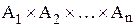) называется множеством всех векторов 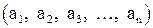, длины n таких, что .

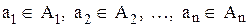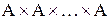обозначается .

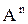Примеры:

1) Множество 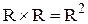- множество точек плоскости, т. е. множество всех пар вида (a, b), где 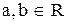и является координатами точек плоскости. Координатное представление точек плоскости предложил Декарт. Это исторически первый пример прямого произведения. Поэтому иногда прямое произведение называется декартовым.

2)

.

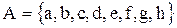
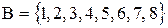Тогда 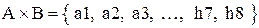- множество, содержащее обозначение всех 64-х клеток шахматной доски.

3) Рассмотрим множество всех числовых матриц 3 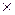4, матриц вида:

,

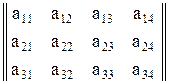где 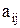Принадлежит множеству R. Строки матрицы - элементы множества 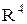(векторы длины 4). Сама матрица рассматривается как упорядоченный набор элементов множества 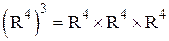. Компоненты матрицы, заданной таким образом - строки, а не числа; 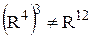. Содержательный смысл этого неравенства в следующем: в векторе 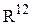нет никакой информации о строении матрицы; тот же вектор 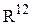мог бы перечислять элементы матрицы 4 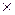3 или 2 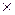6, которые, как математические объекты, вовсе не совпадают с матрицей 4 3.

Итак, компонентами вектора могут быть также и векторы:

.

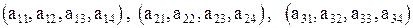4) Пусть А - конечное множество, элементами которого являются символы (буквы, цифры, знаки препинания, знаки операций и т. д.). Такие множества обычно называют алфавитом.

Определение: Слова длины n в алфавите А - это элементы множества .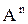

Определение: Множество всех слов в алфавите А - это множество

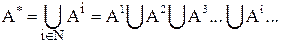
Здесь слово определено как вектор. При написании слова не принято пользоваться разделителями: скобками, запятыми; они могут оказаться символами самого алфавита. Поэтому слово в алфавите обозначается как конечная последовательность символов из алфавита А.

Примеры:

1) Десятичное число – слово в алфавите {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

2) Текст, отпечатанный на машинке, – слово в алфавите, определяемом клавиатурой этой машинки.