Вектор  может быть представлен в виде:
может быть представлен в виде:
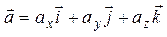 (34)
(34)
 где
где 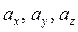 – проекции вектора
– проекции вектора  на оси координат (координаты вектора), векторы
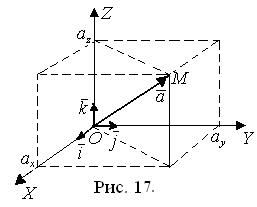
на оси координат (координаты вектора), векторы 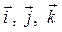 – это орты (единичные векторы) координатных осей (рис. 17).
– это орты (единичные векторы) координатных осей (рис. 17).
Векторную формулу (34) можно писать сокращенно: 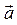 = { ax; ay; az }.
= { ax; ay; az }.
Орты 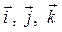 имеют проекции:
имеют проекции:
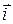 ={1; 0; 0},
={1; 0; 0}, 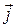 ={0; 1; 0},
={0; 1; 0}, 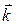 ={0; 0; 1}.
={0; 0; 1}.
Модуль (длина) вектора 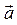 = { ax; ay; az } определяется по формуле:
= { ax; ay; az } определяется по формуле:
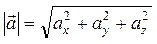 . (35)
. (35)
Координатами точки М называют проекции ее радиус-вектора 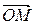 (рис. 17). Обозначают координаты точки М (x; y; x) или М (xМ; yМ; xМ).
(рис. 17). Обозначают координаты точки М (x; y; x) или М (xМ; yМ; xМ).
Расстояние между точками А (xА , yА, zА) и B (xВ, yB, zB,) определяется по формуле:
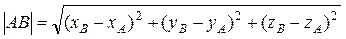 . (36)
. (36)
Если известны координаты точек – начала и конца вектора 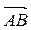 :
:
А (xА , yА, zА), B (xВ, yB, zB), то проекции вектора 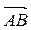 можно найти по формуле:
можно найти по формуле:
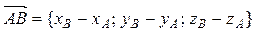 . (37)
. (37)
Пусть даны векторы  = { ax; ay; az } и
= { ax; ay; az } и 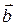 = { bx; by; bz }, тогда проекции суммы (разности) векторов:
= { bx; by; bz }, тогда проекции суммы (разности) векторов:
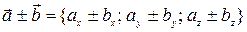 . (38)
. (38)
Произведение вектора на число: если λ – число и 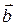 = λ
= λ  , то
, то
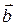 = { λax; λay; λaz }. (39)
= { λax; λay; λaz }. (39)
Скалярное произведение векторов 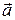 и
и 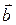 – это число, равное произведению модулей векторов на косинус угла между ними:
– это число, равное произведению модулей векторов на косинус угла между ними:
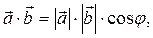
где φ – угол между векторами 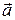 и
и 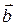 .
.
Другие обозначения скалярного произведения: 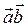 ,
, 
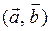 .
.
Если  = { ax; ay; az },
= { ax; ay; az }, 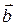 = { bx; by; bz }, то скалярное произведение
= { bx; by; bz }, то скалярное произведение
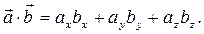 (40)
(40)
При помощи скалярного произведения можно найти угол между векторами:
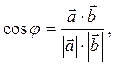 (41)
(41)
а также проекцию одного вектора на ось другого вектора:
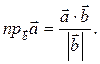 (42)
(42)
Векторное произведение вектора 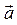 на вектор
на вектор 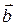 – это вектор
– это вектор 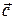 , удовлетворяющий трем условиям:
, удовлетворяющий трем условиям:
1) 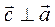 ,
, 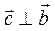 ;
;
2) векторы 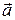 ,
, 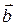 и
и 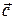 образую правую тройку;
образую правую тройку;
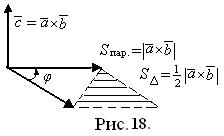
3) 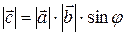 , то есть |
, то есть | 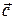 | равен площади параллелограмма, построенного на векторах
| равен площади параллелограмма, построенного на векторах 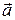 и
и 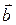 (рис. 18).
(рис. 18).
 Обозначения векторного произведения:
Обозначения векторного произведения: 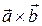 ,
, 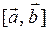 .
.
Если  = { ax; ay; az },
= { ax; ay; az }, 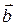 = { bx; by; bz }, то векторное произведение можно вычислить при помощи определителя:
= { bx; by; bz }, то векторное произведение можно вычислить при помощи определителя: 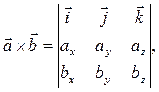
или, с использованием формулы (27):
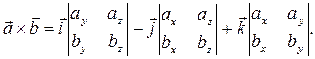 (43)
(43)
Векторное произведение используют, когда нужно найти вектор 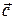 , перпендикулярный двум данным векторам
, перпендикулярный двум данным векторам 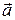 и
и 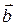 :
: 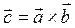 , а также для вычисления площади параллелограмма (или треугольника), построенного на векторах
, а также для вычисления площади параллелограмма (или треугольника), построенного на векторах 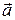 и
и 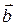 (рис. 18):
(рис. 18):
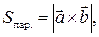
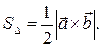 (44)
(44)
Смешанным произведением трех векторов 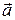 ,
, 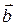 и
и 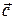 называется число, равное скалярному произведению векторов
называется число, равное скалярному произведению векторов 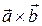 и
и 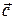 .
.
Обозначения смешанного произведения: 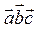 или
или 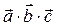 .
.
Если  = { ax; ay; az },
= { ax; ay; az }, 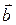 = { bx; by; bz } и
= { bx; by; bz } и 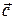 = { сx; сy; сz }, то смешанное произведение можно вычислить при помощи определителя:
= { сx; сy; сz }, то смешанное произведение можно вычислить при помощи определителя:
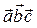 =
= 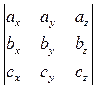 . (45)
. (45)
Если три ненулевых вектора 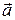 ,
, 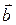 и
и 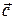 параллельны одной и той же плоскости (компланарны), то их смешанное произведение равно нулю:
параллельны одной и той же плоскости (компланарны), то их смешанное произведение равно нулю:
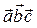 = 0. (46)
= 0. (46)
Объем V параллелепипеда, построенного на векторах 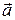 ,
, 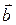 и
и 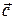 можно вычислить по формуле:
можно вычислить по формуле:
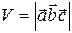 . (47)
. (47)
 2015-02-04
2015-02-04 776
776








