2F0). 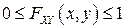 для любых
для любых 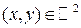 .
.
(Свойство очевидно, так как функция распределения 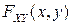 - вероятность).
- вероятность).
2F1). Функция распределения 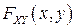 является функцией неубывающей по каждому из своих аргументов.
является функцией неубывающей по каждому из своих аргументов.
▲ Когда один из аргументов 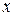 или
или 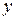 фиксирован, доказательство свойства 2F1) полностью аналогично доказательству свойства F1) в одномерном случае ■.
фиксирован, доказательство свойства 2F1) полностью аналогично доказательству свойства F1) в одномерном случае ■.
2F2). 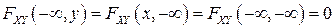 ;
;
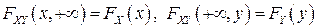 ,
, 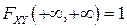 .
.
где 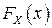 и
и 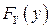 - одномерные функции распределения случайных величин
- одномерные функции распределения случайных величин  и
и  соответственно.
соответственно.
▲ В соответствии со свойствами вероятности
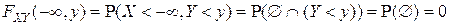 ;
;
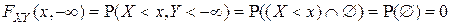 ;
;
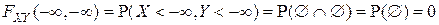 ;
;
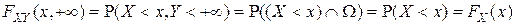 ;
;
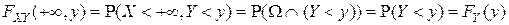 ;
;
В силу аксиомы нормированности Р2)
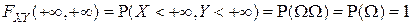
Строгое доказательство свойства 2F2), как и в одномерном случае, основано на использовании аксиомы непрерывности Р4) ■.
Замечание. Смысл равенств 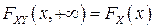 ,
, 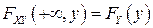 состоит в том, что по функции распределения двумерного случайного вектора
состоит в том, что по функции распределения двумерного случайного вектора  всегда можно найти одномерные (маргинальные) функции распределения его координат
всегда можно найти одномерные (маргинальные) функции распределения его координат 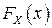 и
и 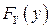 . Обратное без дополнительной информации неверно.
. Обратное без дополнительной информации неверно.
2F3). Функция распределения 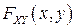 является функцией непрерывной слева по каждому из своих аргументов.
является функцией непрерывной слева по каждому из своих аргументов.
▲ Когда один из аргументов 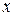 или
или 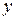 фиксирован, доказательство свойства 2F3) полностью аналогично доказательству свойства F3) в одномерном случае ■.
фиксирован, доказательство свойства 2F3) полностью аналогично доказательству свойства F3) в одномерном случае ■.
2F4). Вероятность попадания случайного вектора  в прямоугольник
в прямоугольник 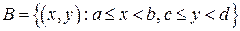 со сторонами, параллельными осям координат, определяется по формуле:
со сторонами, параллельными осям координат, определяется по формуле:

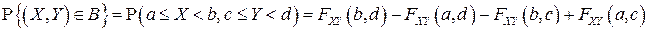
▲ Обозначим
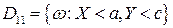 ;
;
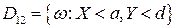 ;
;
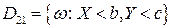 ;
;
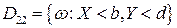 .
.
Очевидно, что 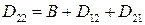 . При этом события
. При этом события 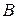 и
и 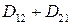 являются несовместными, а
являются несовместными, а 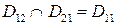 . Поэтому по теореме сложения вероятностей получаем:
. Поэтому по теореме сложения вероятностей получаем:
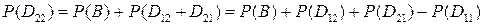 .
.
Осталось учесть, что 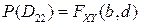 ,
, 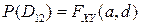 ,
,
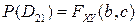 ,
, 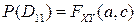 ■.
■.
Замечание. Как отмечалось ранее, свойства F1), F2) и F3) полностью описывают класс одномерных функций распределения. В двумерном случае это уже не так. Наряду с выполнением свойств 2F1), 2F2) и 2F3) для этого необходимо еще выполнение свойства 2F4) (подробности см. в учебнике Боровкова А.А. «Теория вероятностей»).
Замечание. Аналогично одномерному случаю вводится понятие борелевской  -алгебры на плоскости
-алгебры на плоскости 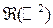 как минимальной
как минимальной 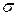 -алгебры, содержащей все прямоугольники вида
-алгебры, содержащей все прямоугольники вида 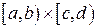 со сторонами параллельными осям координат. Тогда свойство 2F4) совместно с теоремой о продолжении меры позволяет считать, что двумерная функция распределения
со сторонами параллельными осям координат. Тогда свойство 2F4) совместно с теоремой о продолжении меры позволяет считать, что двумерная функция распределения 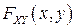 полностью определяет вероятность
полностью определяет вероятность 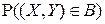 попадания случайного вектора
попадания случайного вектора  в любое борелевское множество
в любое борелевское множество 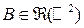 (хотя явного аналитического для
(хотя явного аналитического для 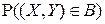 через функцию распределения
через функцию распределения 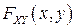 при этом может и не быть).
при этом может и не быть).
Аналогичными являются определение и свойства многомерной функции распределения.
Определение. Функция 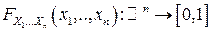
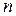 действительных переменных, определяемая для любого
действительных переменных, определяемая для любого 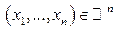 равенством
равенством
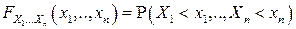 ,
,
называется функцией распределения случайного вектора 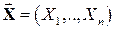 или многомерной (
или многомерной (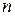 -мерной) функцией распределения или совместной функцией распределения случайных величин
-мерной) функцией распределения или совместной функцией распределения случайных величин 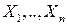 .
.
 2015-06-28
2015-06-28 1960
1960
