Часто в вероятностных моделях случайных явлений приходится рассматривать сразу несколько случайных величин, причем изучение каждой случайной величины отдельно от других приводит к недопустимому упрощению модели явления. Математической моделью таких случайных явлений является понятие случайного вектора.
Определение. Совокупность случайных величин 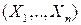 , определенных на одном и том же вероятностном пространстве
, определенных на одном и том же вероятностном пространстве 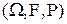 , значения которых совместно описывают результат некоторого случайного эксперимента, называется
, значения которых совместно описывают результат некоторого случайного эксперимента, называется 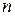 -мерным случайным вектором (многомерной случайной величиной или системой случайных величин) и обозначается
-мерным случайным вектором (многомерной случайной величиной или системой случайных величин) и обозначается 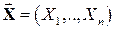 . При этом сами случайные величины
. При этом сами случайные величины 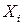 ,
, 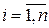 называют координатами (компонентами, составляющими) случайного вектора
называют координатами (компонентами, составляющими) случайного вектора 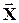 .
.
Как и в одномерном случае, исчерпывающей вероятностной характеристикой случайного вектора является его функция распределения. Рассмотрим вначале случай двумерного случайного вектора 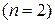 , как наиболее часто встречающийся в практических приложениях, а потом полученные результаты обобщим на случай многомерный.
, как наиболее часто встречающийся в практических приложениях, а потом полученные результаты обобщим на случай многомерный.
Двумерный случайный вектор обычно обозначают 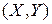 (без введения индексов).
(без введения индексов).
Определение. Функцией распределения случайного вектора 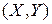 называется функция
называется функция 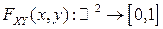 двух действительных переменных
двух действительных переменных 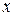 и
и 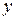 , определяемая при каждом
, определяемая при каждом 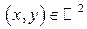 равенством:
равенством:
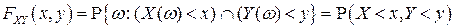 . (3.1)
. (3.1)
Функцию распределения 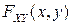 случайного вектора
случайного вектора 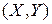 называют также двумерной функцией распределения или совместной функцией распределения случайных величин
называют также двумерной функцией распределения или совместной функцией распределения случайных величин  и
и  .
.
Геометрически функция распределения 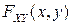 представляет собой вероятность попадания случайной точки
представляет собой вероятность попадания случайной точки 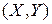 в квадрант с вершиной в точке
в квадрант с вершиной в точке 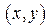 .
.

Из определения (3.1) следует, что функция распределения 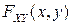 случайного вектора
случайного вектора 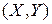 определена на всей плоскости
определена на всей плоскости 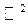 .
.
Действительно, множество 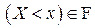 при любом
при любом 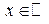 по определению случайной величины
по определению случайной величины  . Множество
. Множество 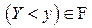 при любом
при любом 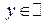 по определению случайной величины
по определению случайной величины  . Поэтому произведение этих множеств
. Поэтому произведение этих множеств 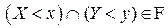 при любых
при любых 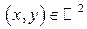 по определению
по определению
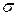 -алгебры
-алгебры 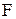 .
.
 2015-06-28
2015-06-28 5774
5774