Понятие о моментах

Наряду с рассмотренными выше числовыми характеристиками случайных векторов, в приложениях используются также и моменты более высоких порядков.

Если задан случайный вектор 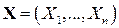, то величины

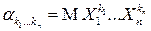и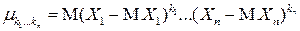

называются начальными и центральными смешанными моментами порядка 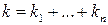соответственно (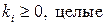). Вычисляются моменты более высоких порядков по формулам для 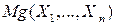, вытекающим из обобщения ОТМО на многомерный случай.

В частности,

.

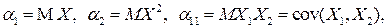
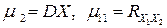Пример 1. Закон распределения случайного вектора задан таблицей:

-1	0,1	0,2
	0,3		0,1
	0,1	0,2

Найти: 1) законы распределения случайных величин и . Являются ли случайные величины и независимыми?

2) корреляционную матрицу. Являются ли случайные величины и некоррелированными?

3) условный закон распределения случайной величины при условии, что случайная величина приняла значение, равное 0; вычислить 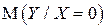и .

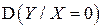Решение. 1) Для случайной величины вероятности её значений 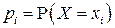находятся суммированием вероятностей 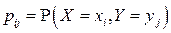в 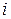-ой строке таблицы ():

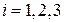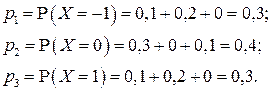
Поэтому закон распределения случайной величины имеет вид:

	-1
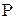
	0,3	0,4	0,3

Вероятности значений случайной величины 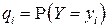находятся суммированием вероятностей 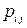в 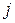-ом столбце таблицы ():

.

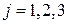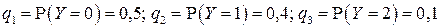Поэтому закон распределения случайной величины имеет вид:

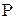
	0,5	0,4	0,1

Условием независимости случайных величин и является равенство:

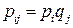, для всех .

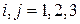Поскольку в данном случае

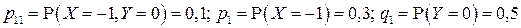, то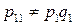

и, следовательно, случайные величины и зависимы.

2) Найдем математические ожидания случайных величин и , используя одномерные законы распределения:

;

.

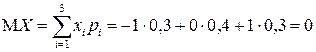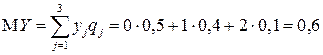Найдем далее дисперси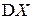и и 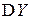по одномерным законам распределения:

;

.

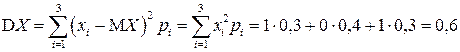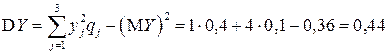Корреляционный момент 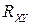находится только по совместному закону распределения случайных величин и :

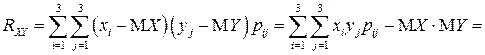
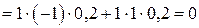(отсутствующие слагаемые равны 0).

Поскольку корреляционный момент 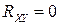, то случайные величины и являются некоррелированными.

Корреляционная матрица имеет вид:

.

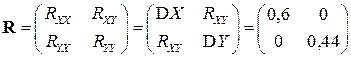3) Условный закон распределения случайной величины при условии, что случайная величина 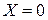определяется совокупностью условных вероятностей:

,

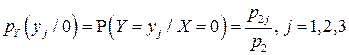которые равны: .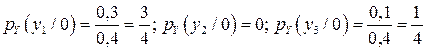

Записывается условный закон распределения случайной величины при условии, что случайная величина 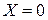в виде таблицы:

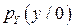
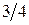
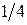
Найдем условное математическое ожидание :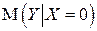

.

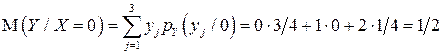Условная дисперсия 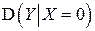вычисляется по формуле:

.

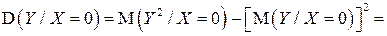
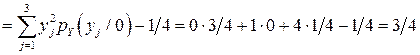Пример 2. Плотность вероятностей 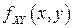двумерного случайного вектора имеет вид:

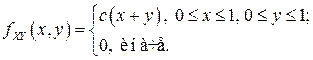
Найти:

а) коэффициент ;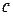

б) функцию распределения ;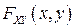

в) плотности вероятностей координат 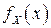и ;

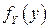г) условные плотности вероятносте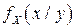й и ;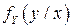

д) математическое ожидание и корреляционную матрицу вектора ;

е) вероятность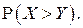

Являются ли случайные величины и независимыми? Являются ли они некоррелированными?

Решение. а) Коэффициент 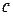определяется из условия нормировки:

.

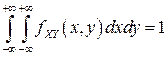В данном случае это условие означает, что

.

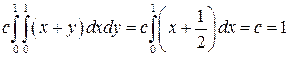б) Функция распределения 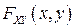связана с двумерной плотностью вероятностей соотношением:

.

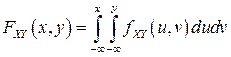При 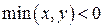имеем:

.

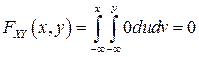При 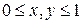имеем:

.

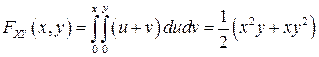Пр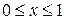и и 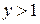имеем:

.

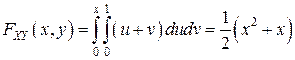Заметим, что в данной области 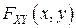в соответствии со свойством 5) совпадает с функцией распределения 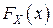случайной величины .

Пр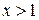и и 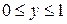имеем:

.

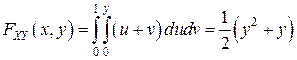В данной области 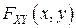совпадает с функцией распределения 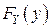случайной величины .

Пр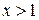и и 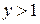имеем:

.

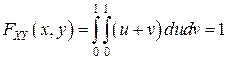Окончательно для функции распределения получаем выражение:

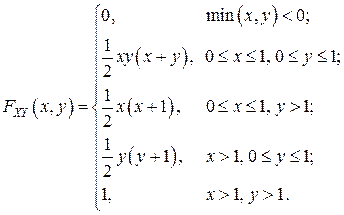
в) Найдём плотности вероятностей координат 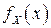и :

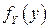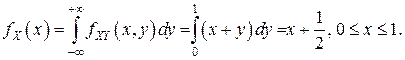
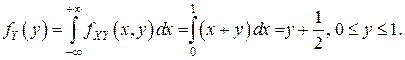
г) Условные плотности вероятносте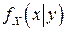й и 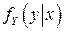находятся по формулам:

.

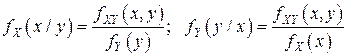В данном случае

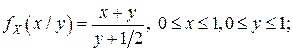
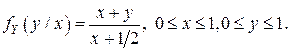
д) Найдём математические ожидания 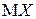и 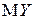и дисперси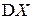и и 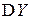, воспользовавшись одномерными законами распределения:

;

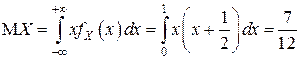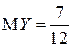в силу симметрии.

;

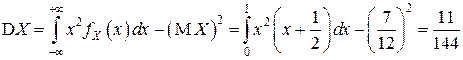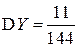в силу симметрии.

Корреляционный момент 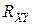находится по совместной плотности вероятностей случайных величин и :

.

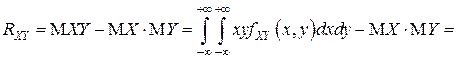
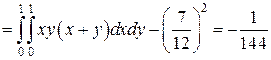Корреляционная матрица вектора имеет вид:

.

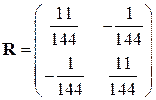е) Вероятность 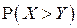вычисляется по формуле:

,

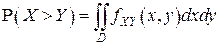где область .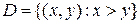

Интегрируя, получаем:

.

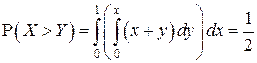Поскольку 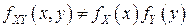, то случайные величины и являются зависимыми. Корреляционный момент 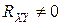, поэтому случайные величины являются коррелированными.