Определение. Случайные величины  и
и  , для которых корреляционный момент
, для которых корреляционный момент 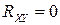 , называются некоррелированными.
, называются некоррелированными.
Учитывая, что
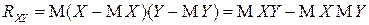 ,
,
получаем: случайные величины  и
и  являются некоррелированными тогда и только тогда, когда
являются некоррелированными тогда и только тогда, когда 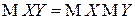 .
.
Отсюда и из теоремы 2 вытекает, что из независимости случайных величин всегда следует их некоррелированность. Обратное, вообще говоря, неверно. Можно только сказать, что если случайные величины являются коррелированными, так, что 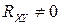 , то они являются зависимыми.
, то они являются зависимыми.
Пример.
Равномерное распределение в круге 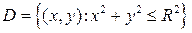 .
.
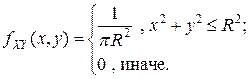
Ранее были найдены одномерные плотности вероятностей координат вектора  :
:
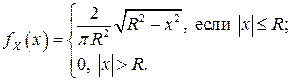
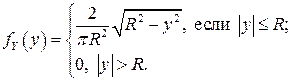
и установлено, что случайные величины  и
и  являются зависимыми, так как
являются зависимыми, так как 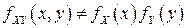 .
.
Найдем корреляционный момент 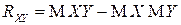 СВ
СВ  и
и  .
.
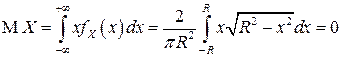
в силу нечетности подинтегральной функции и симметричности относительно нуля пределов интегрирования.
По аналогичным соображениям 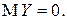 Найдем
Найдем 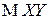 .
.
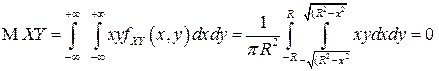
также в силу нечетности подинтегральной функции.
Таким образом, 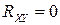 и, следовательно, случайные величины
и, следовательно, случайные величины  и
и  являются зависимыми, но некоррелированными.
являются зависимыми, но некоррелированными.
Понятие некоррелированности случайных величин играет важную роль в теории вероятностей. Подтверждением тому является следующая теорема.
Теорема 3 (теорема сложения дисперсий).
Для любых действительных чисел 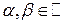 и любых случайных величин
и любых случайных величин  и
и  , имеющих конечную дисперсию
, имеющих конечную дисперсию
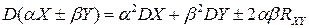 .
.
В частности, если 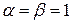 и случайные величины
и случайные величины  и
и  являются некоррелированными, то имеет место свойство аддитивности дисперсии:
являются некоррелированными, то имеет место свойство аддитивности дисперсии:
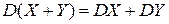 .
.
▲ Доказательство теоремы основано только на свойствах математического ожидания и определении корреляционного момента 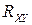 :
:
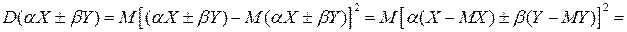
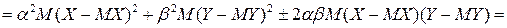
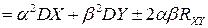 .■.
.■.
По индукции утверждение теоремы 3 обобщается на линейную комбинацию любого конечного числа случайных величин следующим образом.
Для любых действительных чисел 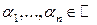 и случайных величин
и случайных величин  , имеющих конечную дисперсию
, имеющих конечную дисперсию
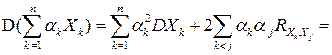
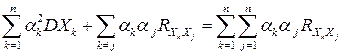 .
.
В частности, если все 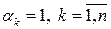 , а случайные величины
, а случайные величины  являются попарно некоррелированными (
являются попарно некоррелированными (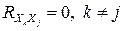 ), то имеет место свойство аддитивности дисперсии:
), то имеет место свойство аддитивности дисперсии:
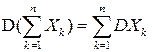 .
.
 2015-06-28
2015-06-28 7138
7138
