Соприкасающаяся плоскость. Естественный трехгранник Френе

Соприкасающейся плоскостью к кривой 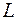в ее точке 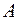называется предельное положение касательной.

Если кривая 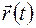имеет непрерывную производную 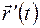в окрестности точки 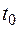и вторую производную 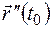такую, что 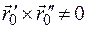, то соприкасающаяся плоскость к этой кривой в точке 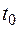существует и имеет уравнение

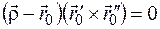, (1.22)

где радиус−вектор текущей точки плоскости.

Из точки 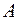кривой 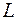можно выпустить три единичных вектора 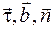, определяющих естественную прямоугольную систему координат в окрестности точки :

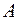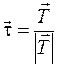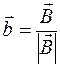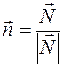, , , (1.23)

где , , .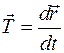

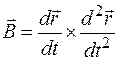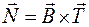Здесь 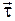− единичный вектор касательной, направление 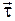зависит от от параметра ;

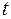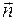− единичный вектор главной нормали, направлен в сторону вогнутости кривой;

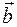− единичный вектор бинормали, определяется как перпендикуляр к векторам 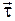и 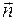, и направлен так, что вектора 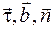образуют правую тройку векторов.

Приложенные к движущейся по кривой точке 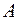векторы 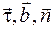образуют естественный трехгранник Френе.