2015-06-28
1956
Пусть в ДСК задана гладкая кривая, определяемая вектором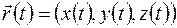 
, 
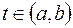. Будем считать, что отсчет дуги выбран так, что ее длина возрастает вместе с возрастанием параметра 
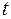. Положим 
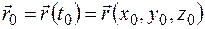и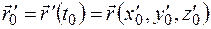 
.
Вектор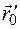 
имеет направление касательной к кривой в точке 
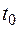и поэтому произвольная точка касательной 
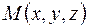определяется вектором
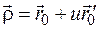, (1.15)
где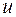 
− произвольное число (текущий параметр касательной) (рис. 1.3).
Равенство (1.15) − уравнение касательной к кривой в точке 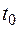в векторной форме.
Из (1.15) следует, что уравнения касательной в декартовой системе координат имеют вид:
, 
, 
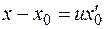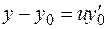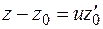
или
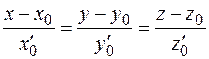. (1.16)
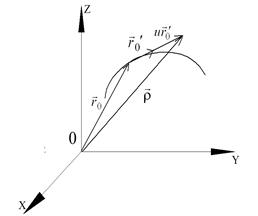
Рис. 1.3
Обозначим через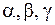 
углы, которые образует положительное направление касательной соответственно с положительными направлениями осей координат 
:
,
,
,
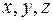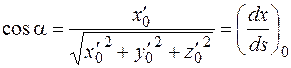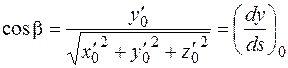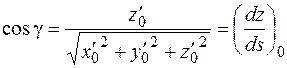где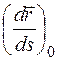 
обозначает, что в 
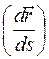нужно подставить значение 
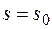соответствующее 
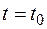. Перед корнем стоит знак плюс, т.к. мы согласились, что длина дуги возрастает вместе с . 
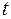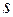− строго возрастающая функция, отображающая интервал 
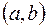изменения 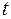на некоторый интервал 
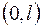изменения .
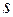Кривую, заданную в плоскости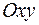 
, можно рассматривать как частный случай кривой в пространстве, у которой 
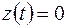. Поэтому соотношениям (1.16) в данном случае соответствует одно уравнение
.
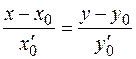Положительное направление касательной образует с осью 
угол 
, для которого
, 
.
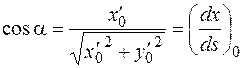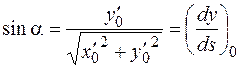В плоском случае можно определить понятие нормали в точке 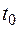кривой, т.е. прямой, принадлежащей рассматриваемой плоскости и проходящей через точку 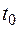перпендикулярно к касательной. Направление вектора нормали 
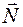задается таким образом, чтобы вектор касательной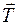 
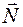и вектор нормали образовали систему направленную так же как и система координат 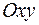(рис 1.4,1.5).
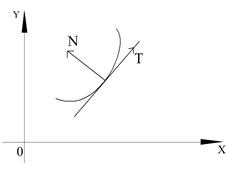
Рис. 1.4 Рис. 1.5
Для пространственной кривой вводится понятие нормальной плоскости − плоскость, проходящая через точку касания перпендикулярно касательной. Так как плоскость перпендикулярна касательной, то направляющий вектор последней будет являться нормальным вектором плоскости. Поэтому уравнение касательной плоскости будет иметь вид:
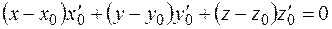. (1.17)
