Пример. Дан радиус-вектор движущийся в пространстве точки 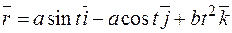 (
(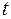 - время,
- время, 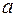 и
и 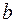 - постоянные). Найти годографы скорости и ускорения.
- постоянные). Найти годографы скорости и ускорения.
Скорость движущейся точки вычисляется по формуле 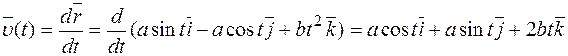
Чтобы построить годограф 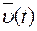 положим, что
положим, что
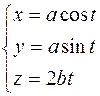 , это параметрическое задание винтовой линии, т.е. годограф
, это параметрическое задание винтовой линии, т.е. годограф 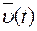 − винтовая линия.
− винтовая линия.
Найдем годограф ускорения 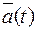
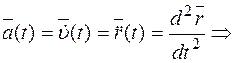
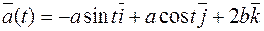 .
.
Следовательно, годограф 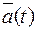 линия заданная параметрически следующим образом
линия заданная параметрически следующим образом 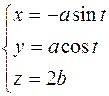 , это параметрические задание окружности, т.е. годограф ускорения
, это параметрические задание окружности, т.е. годограф ускорения 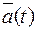 - окружность.
- окружность.
Пример. Дано 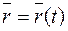 . Найти производные
. Найти производные
а) 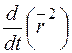 ; б)
; б) 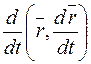 ; в)
; в) 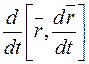
а) Используем правило дифференцирования скалярного произведения
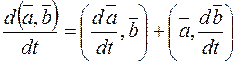 , т.к.
, т.к. 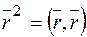 , следовательно
, следовательно 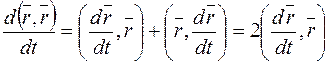 .
.
б) Аналогично примеру а) получаем
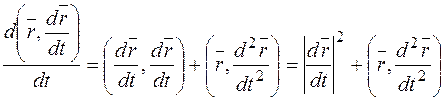
в) Используем правило дифференцирования векторного произведения
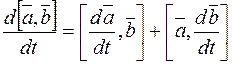 , тогда
, тогда
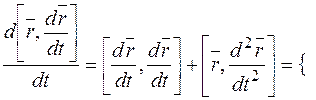 т.к.
т.к. 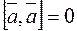
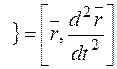
Пример. Найти радиус кривизны линии 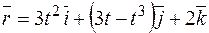 при
при 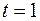 .
.
Кривизна линии заданной векторно-параметрическим уравнением 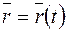 , где параметр
, где параметр 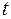 – произвольный, определяется по формуле
– произвольный, определяется по формуле
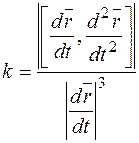 , где
, где 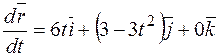 ,
,
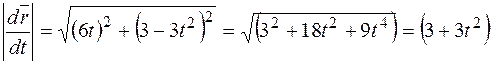 ,
,
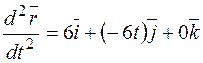 .
.
Вычислим векторное произведение
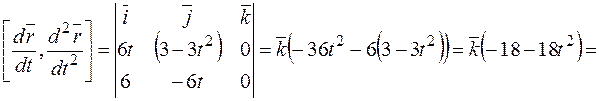
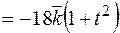 .
.
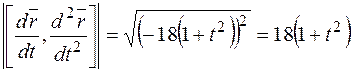 . Тогда
. Тогда 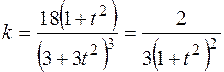 , и
, и 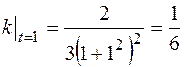 . Следовательно, радиус кривизны равен
. Следовательно, радиус кривизны равен 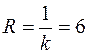 .
.
Пример. Написать уравнение соприкасающейся плоскости в точке 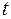 =0 кривой
=0 кривой 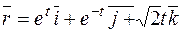 .
.
Векторное уравнение соприкасающейся плоскости к кривой 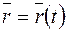 в точке
в точке 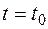 имеет следующий вид:
имеет следующий вид:
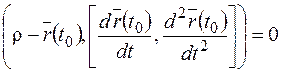 .
.
Найдем частные производные первого и второго порядка 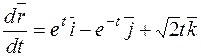 ,
, 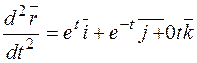 .
.
Вычислим векторное произведение найденных функций и посчитаем его значение при 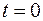 :
:
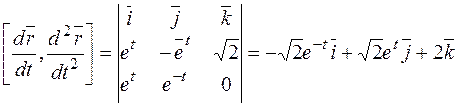 ,
, 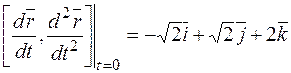
Так как вектор 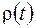 равен:
равен: 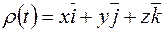 , то уравнение соприкасающейся плоскости имеет вид:
, то уравнение соприкасающейся плоскости имеет вид:
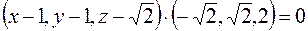 или
или 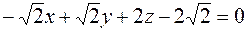 .
.
Пример. Найти кручение в любой точке 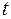 кривой
кривой 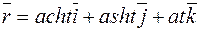 .
.
Кручение кривой заданной вектор функцией 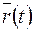 определяется по следующей формуле:
определяется по следующей формуле:
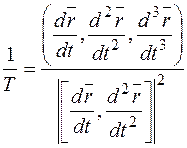 .
.
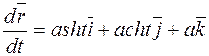 ,
, 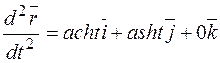 ,
,
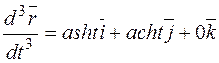 .
.
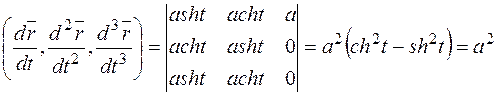
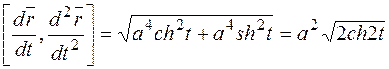 , тогда
, тогда
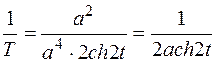 .
.

 2015-06-28
2015-06-28 2085
2085








