2015-06-28
765
Вектор-функция скалярного аргумента
Определение. Если каждому значению параметра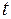 
из некоторого промежутка отвечает определенный вектор 
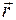(зависящий от 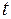), то вектор 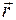называется векторной функцией (кратко вектор-функция) от скалярного аргумента 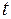и в этом случае пишут:
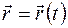. (1.1)
При изменении аргумента 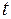вектор 
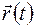изменяется как по величине, так и по направлению. В дальнейшем будем предполагать, что 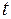изменяется в промежутке, конечном или бесконечном.
Будем считать, что вектор 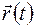исходит из начала координат, т.е. 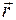− радиус-вектор некоторой точки 
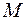. В этом случае при изменении параметра 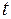конец вектора 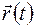опишет линию 
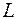, называемую годографом векторной функции 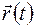. При этом начало координат называют полюсом годографа. Уравнение (1.1) называют векторным уравнением кривой 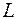(рис. 1.1).
Если у вектора 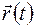меняется только модуль, то годографом его будет луч, исходящий из полюса. Если модуль вектора 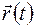постоянен и меняется только его направление, то годограф есть линия, лежащая на сфере с центром в полюсе и радиусом, равным модулю вектора .
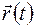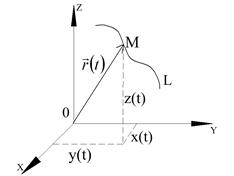
Рис. 1.1
Если через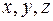 
обозначить проекции вектора 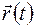на оси прямоугольной декартовой системы координат в пространстве, то эти величины для каждого значения параметра 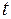в свою очередь принимают определенные числовые значения и поэтому являются скалярными функциями скалярного аргумента :
, 
, 
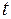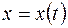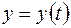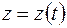. (1.2)
И тогда
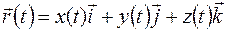. (1.3)
Таким образом, задание векторной функции скалярного аргумента равносильно заданию трех скалярных функций того же аргумента. Т.к. уравнение (1.1) является уравнением некоторой кривой в пространстве, то ту же кривую задают уравнения (1.2). Уравнения (1.2) − обычные параметрические уравнения кривой в пространстве.
Пример. Рассмотрим кривую, заданную параметрически с помощью уравнений
, 
, 
.
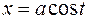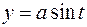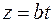Эта кривая называется винтовой линией. Ее векторное уравнение
.
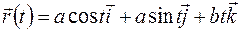При любом значении параметра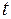 
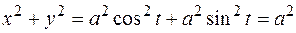. Это означает, что винтовая линия расположена на цилиндре 
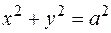. Отсюда следует, что, когда точка 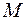движется по винтовой линии, ее проекция 
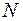на плоскости 
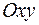перемещается по окружности радиуса 
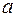и с центром в начале координат, причем 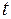является полярным углом точки 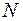. Когда точка 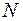описывает полную окружность, аппликата 
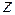точки 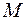винтовой линии увеличивается на 
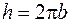. Эта величина называется шагом винтовой линии.
Вектор функция скалярного аргумента.
Отображение f: x→у – называется вектор-функцией скалярного аргумента если х принадлежит R, y принадлежит R. Для t принадлежащего х соответствующее значение ф-ции обозначается r=f(t). из определения следует, что задание одной вектор функции равносильно заданию n скалярных функций.
{X1= f1(t)
{X2=f2(t)
{X3=f3(t)
{Xn=fn(t)
Рассмотрим частный случай
{X=f(t)
{Y= (t) (1)
Величина t называется параметром, поэтому уравнение (1) параметрическими уравнениями плоской кривой. Если из уравнения (1) исключить параметр t, то приходим к уравнению плоской кривой в неявном виде F(x,y)= 0 (2), которое в некоторых случаях разрешить относительно Y, т.е. y=f(x) (3). Таким образом (1)-(3) различные формы записи уравнения плоской кривой.
Пример: установить, какая кривая задана следующими параметрическими уравнениями
{X=a cost=> cost = x/a
{Y=b sin t=> sin t= y/b
X^2/a^2 + y^2/b^2=1 получим неявное уравнение эллипса
Y=± b/a корень a^2-x^2
