2015-06-28
1256
Кривизной окружности радиуса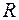 
называется число 
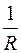. Это число можно получить как отношение угла между касательными в концах какой-либо дуги окружности к длине этой дуги.
Последнее утверждение дает возможность определения кривизны для произвольной гладкой кривой.
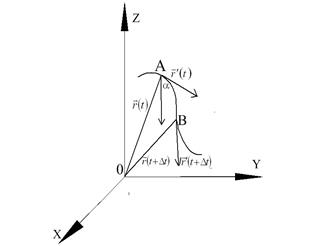Рассмотрим гладкую кривую 
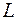. Угол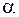 
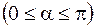называется углом смежности дуги 
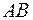. Отношение угла смежности дуги 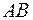к ее длине называется средней кривизной дуги 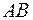(рис. 1.6).
Рис. 1.6
Кривизной кривой 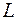в ее точке 
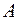называется предел (конечный или бесконечный) отношения угла смежност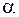и дуги 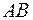кривой к ее длине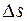 
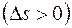, когда последняя стремится к нулю
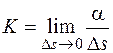. (1.18)
Таким образом 
. По определению, величина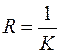 
называется радиусом кривизны 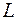в точке .
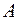Угол смежност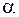и дуги 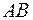равен углу между векторам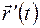и 
и 
. Из векторной алгебры известно, что
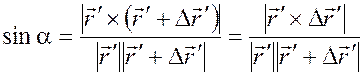. (1.19)
Знаменатель в выражении (1.19) не равен нулю. Поэтому при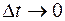 
знаменатель стремится к 
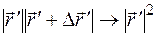, а числитель стремится к нулю.
Будем теперь предполагать, что радиус−вектор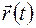 
кривой имеет вторую производную 
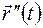, и при этом условии докажем существование конечной кривизны в точке .
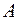В силу (1.18), (1.19) кривизна в точке равна
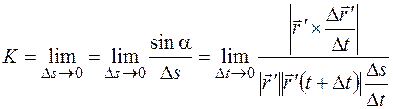, (1.20)
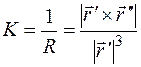. (1.21)
Кручением кривой называется величина равная
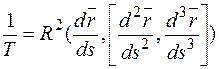. (1.22)
