1. 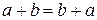 .
.
2. 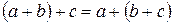 .
.
3. 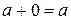 , так как
, так как 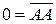 .
.
4. Для каждого вектора 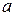
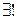 вектор, называемый вектором, противоположным
вектор, называемый вектором, противоположным 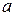 , такой, что
, такой, что 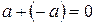 . Доказательство свойств может быть проиллюстрировано рис.2
. Доказательство свойств может быть проиллюстрировано рис.2
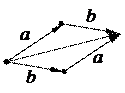 |
 а) б)
а) б) Рис.2. Свойства сложения векторов: а) коммутативность, б) ассоциативность
Если 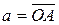 , то через
, то через 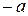 обозначим
обозначим 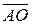 . Тогда
. Тогда 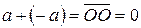 .
.
Определение 10. Произведением вектора 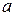 на число
на число 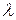
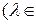 R,
R, 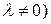 называется вектор
называется вектор 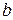 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) векторы 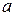 и
и 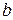 сонаправлены, если
сонаправлены, если 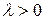 и противоположно направлены, если
и противоположно направлены, если 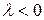 ;
;
2) 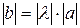 .
.
Произведение вектора на число 0 есть нулевой вектор. Пишут 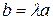 .
.
 2015-06-28
2015-06-28 804
804








