1) Коммутативность: 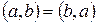 .
.
Действительно, 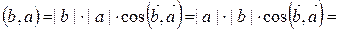 (так как
(так как 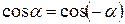 , то есть четная функция, то
, то есть четная функция, то  )
) 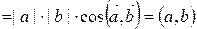 .
.
2) Скалярное произведение двух векторов равно длине одного вектора умноженной на проекцию другого на направление первого.
Действительно, 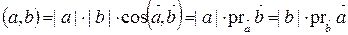 .
.
Отсюда видно, что если 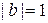 , то
, то 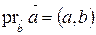 .
.
Следовательно, проекция вектора на ось равна скалярному произведению этого вектора на направляющий вектор оси.
3) 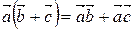 .
.
Действительно, 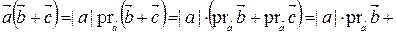
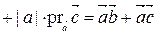 .
.
4) 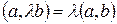 .
.
Действительно, 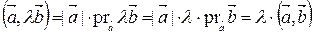 .
.
5) Для того, что бы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю.
 Пусть
Пусть 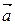 ^
^ 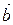 Þ
Þ 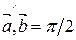 Þ
Þ 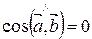 Þ
Þ 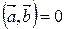 .
.
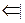 Пусть
Пусть 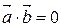 Þ
Þ 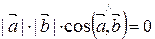 , так как
, так как 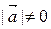 ,
, 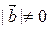 Þ
Þ 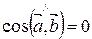 Þ
Þ 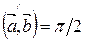 Þ
Þ 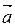 ^
^ 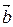 .
.
6) Пусть 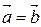 Þ
Þ 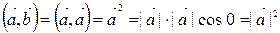 , т.е.
, т.е. 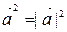 Þ скалярный квадрат вектора
Þ скалярный квадрат вектора 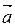 равен квадрату длины вектора Þ
равен квадрату длины вектора Þ 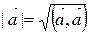 .
.
Из последнего свойства следует, что  – отдельная строка.
– отдельная строка.
7) Пусть в пространстве геометрических векторов задан ортонормированный базис 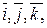 т.е.
т.е. 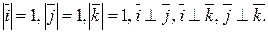 Тогда
Тогда 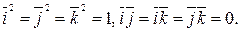
Если вектора 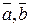 заданы своими координатами
заданы своими координатами 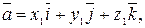
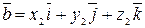 , то
, то
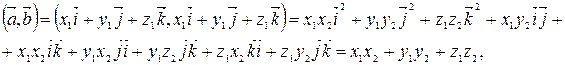
т.е. в прямоугольной декартовой системе координат скалярное произведение векторов равно сумме произведений соответствующих координат.
Из свойства 7) вытекают некоторые метрические формулы:
1) 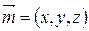 Þ
Þ 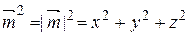 Þ
Þ 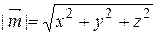
2) Если 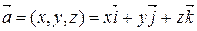 , то
, то 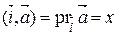 ,
, 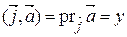 ,
, 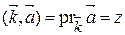 .
.
Таким образом, прямоугольные координаты вектора есть его ортогональные проекции на оси прямоугольной системы координат.
3) Пусть 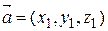 ,
, 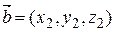 Þ
Þ
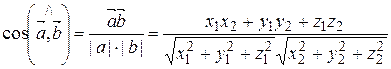 .
.
Таким образом, 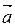 ^
^ 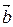 Û
Û 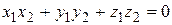 .
.
Из формулы косинуса угла между векторами легко найти углы a, b, g, которые вектор 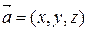 образует с осями координат. Эти углы называются направляющими углами.
образует с осями координат. Эти углы называются направляющими углами.
Имеем:
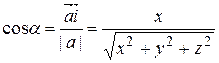 ,
, 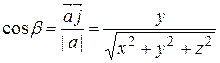 ,
, 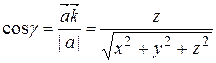 .
.
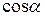 ,
, 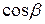 ,
, 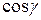 называются направляющими косинусами вектора
называются направляющими косинусами вектора 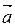 . Они связаны соотношением
. Они связаны соотношением
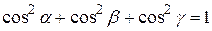 .
.
Следовательно, вектор 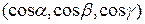 есть координаты вектора
есть координаты вектора 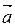 , то есть вектора
, то есть вектора 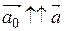 и
и 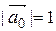 .
.
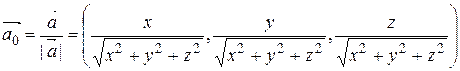 .
.
5о.  Векторное и смешанное произведения векторов.
Векторное и смешанное произведения векторов.
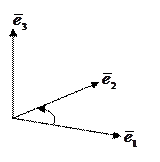 Определение 15. Упорядоченная тройка некомпланарных векторов
Определение 15. Упорядоченная тройка некомпланарных векторов 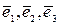 называется правоориентированной или просто правой, если из конца третьего вектора
называется правоориентированной или просто правой, если из конца третьего вектора 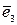 кратчайший поворот от первого
кратчайший поворот от первого 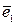 ко второму
ко второму  виден против часовой стрелки. В противном случае тройка называется левоориентированной или левой.
виден против часовой стрелки. В противном случае тройка называется левоориентированной или левой.

Рис. 10. Ориентированные тройки векторов
а) Правая тройка б) Левая тройка
Определение 16. Векторным произведением двух векторов 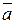 и
и 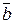 называется вектор
называется вектор 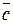 , удовлетворяющий условиям:
, удовлетворяющий условиям:
1) 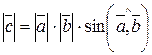 .
.
2) вектор 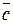 ортогонален векторам
ортогонален векторам 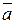 и
и 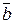 .
.
3) вектора 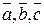 образуют правую тройку векторов.
образуют правую тройку векторов.
Обозначение: 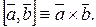
 2015-06-28
2015-06-28 776
776








