1) Длина вектора 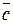 численно равна площади параллелограмма, построенного на векторах
численно равна площади параллелограмма, построенного на векторах 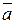 и
и 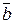 .
.
Доказательство следует из определения 16.
2) Векторное произведение векторов равно нулю тогда и только тогда, когда сомножители коллинеарны.
Доказательство аналогично свойству 5 скалярного произведения.
3) Векторное произведение антикоммутативно, т.е. 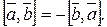
Доказательство.
Тройка 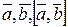 – правая,
– правая, 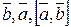 – левая. Тройка будет правой, если изменить направление
– левая. Тройка будет правой, если изменить направление 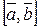 , т.е.
, т.е. 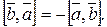 ∎
∎
Пример. Если 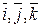 – правая тройка, то
– правая тройка, то 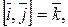
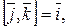
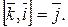
Далее базис всегда будем рассматривать правый.
4) 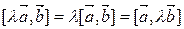 .
.
Докажем первое равенство.
a) Вначале покажем равенство модулей.
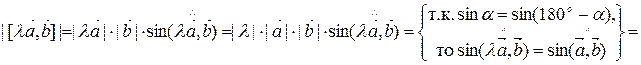
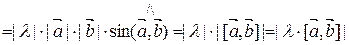 .
.
b) Так как 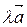 ||
|| 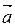 , то
, то 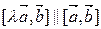
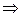
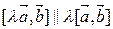 .
.
c) Покажем, что 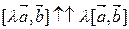 . Рассмотрим случай
. Рассмотрим случай 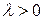 и
и 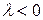 .
.
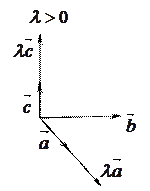
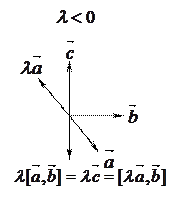
Отсюда вытекает доказываемое свойство.
Определение 17. Смешанным произведением векторов 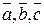 называется число
называется число 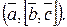
Обозначение: 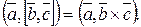
 2015-06-28
2015-06-28 598
598








