Коллинеарные векторы

Определение. Два вектора и называются коллинеарными, если они расположены или на параллельных прямых, или на одной и той же прямой.

Так как направление нулевого вектора произвольно, то он коллинеарен любому вектору.

Теорема. Два ненулевых вектора и коллинеарны тогда и только тогда, когда они пропорциональны, т.е. .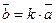

Доказательство. Необходимость. Пусть и коллинеарны, 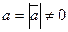, 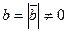. Тогда 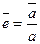и 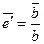. Следовательно, 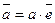и 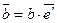. Так как и коллинеарны, то 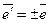и 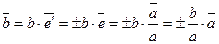. Обозначим 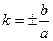, тогда .

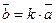Достаточность. Пусть выполнено равенство 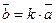, тогда из определения умножения вектора на скаляр следует, что направление вектора или совпадает с направлением , или ему противоположно, а это значит, что и лежат на одной прямой, поэтому коллинеарные. □

6.4. Компланарные векторы

Определение. Три вектора 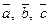называются компланарными, если они или параллельны некоторой плоскости, или лежат на ней.

Теорема. Три ненулевых вектора 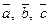компланарны тогда и только тогда, когда один из них является линейной комбинацией других, т.е. .

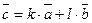Доказательство. Необходимость. Пусть 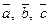‑ компланарные, следовательно, лежат в одной плоскости. Приведём их к общему началу. Рассмотрим два случая.

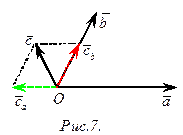
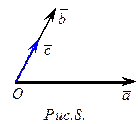
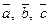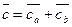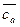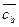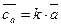1. ‑ попарно не коллинеарны (рис.7), тогда . Так как коллинеарен , коллинеарен , то и 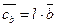. Следовательно, .

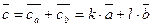2. ‑ попарно коллинеарны, тогда, например, если коллинеарен (рис.8), то .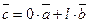

Достаточность. Пусть выполняется равенство 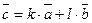. Из определения сложения векторов следует, что вектор 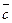лежит в одной плоскости с векторам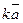и и 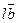, поэтому 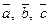‑ компланарные. □

6.5. Ориентация трех некомпланарных векторов в пространстве.

Тройка векторов 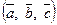называется упорядоченной если известно какой из них первый, второй, третий.

Определение 1. Упорядоченная тройка векторов 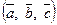имеет правую ориентацию, если:

1) 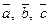‑ некомпланарные;

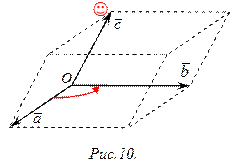
2) после приведения векторов к общему началу, они располагаются так, что кратчайший поворот вектора к вектору виден против часовой стрелки из конца вектора 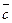(рис.10).

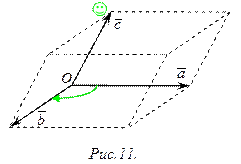
Определение 2. Упорядоченная тройка векторов 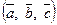имеет левую ориентацию, если:

1) 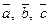‑ некомпланарные;

2) после приведения векторов к общему началу, они располагаются так, что кратчайший поворот вектора к вектору виден по часовой стрелке из конца вектора 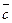(рис.11).

Циклические перестановки векторов не меняют ориентацию и тройки. Например, если 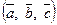правая тройка, то тройки 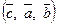, 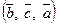‑ правые (рис.12).

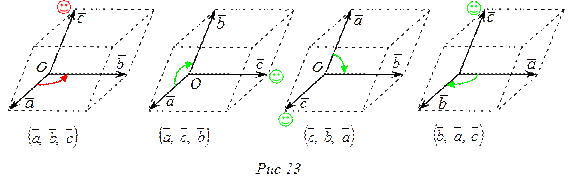
Любая нециклическая перестановка меняет ориентацию тройки. Например, если 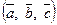‑ правя, то , , 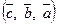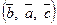‑ левые (рис.13).