Канонический базис квадратичной формы

Базис 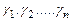пространства 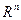называется каноническим базисом квадратичной формы 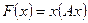, есл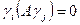и при 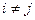. Если 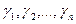– канонический базис 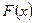, то выражение

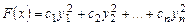, где 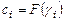называется каноническим видом 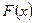в базис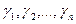е , где 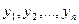– новый набор неизвестных.

Теорема. Если 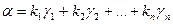– разложение вектора a по каноническому базису 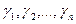квадратичной формы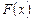 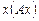, то значение 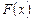на векторе a вычисляется по формуле , .

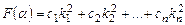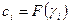Доказательство: рассмотрим следующую цепочку равенств

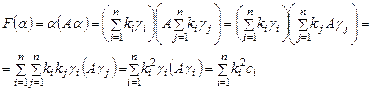
Доказанная теорема утверждает, что если известен канонический базис 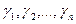квадратичной формы 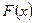и ее канонический вид в этом базисе, то для вычисления значения 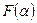квадратичной формы 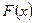на векторе 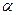достаточно:

1. Разложить a по каноническому базису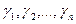

.

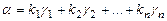2. Коэффициенты разложения 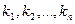подставить вместо неизвестных 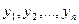в канонический вид.

Квадратичная форма имеет много разных канонических базисов. Процесс построения канонического базиса называется приведением квадратичной формы к сумме квадратов.

Теорема. Ортонормированный базис пространства 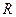, состоящий из собственных векторов 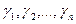симметрической матрицы , , 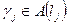где 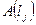– множество всех собственных векторов матрицы порядка 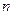, принадлежащих ее собственным значениям 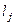, является каноническим базисом квадратичной формы 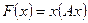, а выражение 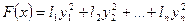– ее каноническим видом в базисе .

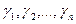Доказательство: Убедимся сначала, что 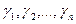– канонический базис 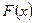. Имеем 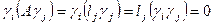, если 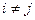, так как 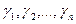ортонормированная система векторов.

Вычислим теперь коэффициенты ее в каноническом виде: 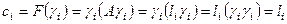, так как система векторов 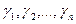нормированная, то , .

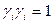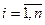Итак, доказано, что если 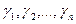– ортонормированный базис из собственных векторов симметрической матрицы , то в этом базисе квадратичная форма 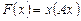имеет вид 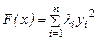, где 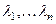– собственные значения матрицы .

Пример 1. Найти канонический вид и канонический базис квадратичной формы 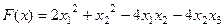в ортонормированном базисе из собственных векторов матрицы

.

.

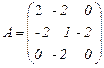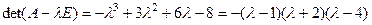Собственные значения матрицы: 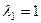, , 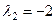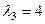. Найдем 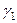, , 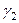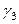. Составим систему уравнений :

.

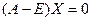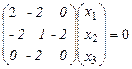Решение имеет вид

, = .

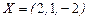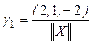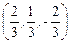Также находим 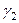, решая систему

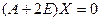
и нормируя решение .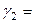

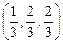Решая уравнение ,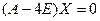

получаем = .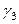

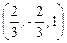Заметим, что эти векторы ортогональны, так как матрица симметрическая.

В базисе 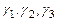форма имеет вид .

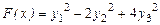Рассмотрим еще один метод построения канонического базиса и канонического вида квадратичной формы (метод Якоби). Будем говорить, что матрица 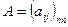удовлетворяет условию Якоби, если определители

, ,

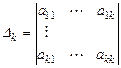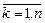называемые угловыми минорами матрицы , не равны 0. Заметим, что 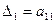, 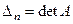. Обозначим через 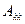матрицу

.

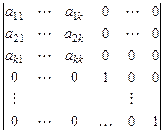
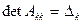Из условия 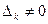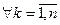следует, что 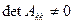. Следовательно, каждая система уравнений

,

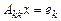
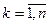где 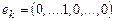– k-й вектор диагональной системы, – имеет единственное решение , .

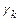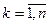Система векторов 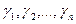называется системой векторов Якоби матрицы , которая удовлетворяет условию Якоби.

Пример 2. Найти систему векторов Якоби для формы, которая рассматривалась в примере 1.

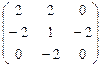
Сначала убедимся, что матрица удовлетворяет условию Якоби

; ,

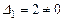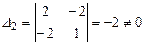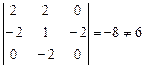
Вектор 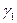является решением системы уравнений

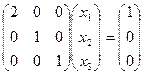
Единственное ее решение – вектор .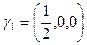

Вектор 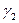является решением системы

.

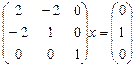Методом Гаусса находим ее решение:

.

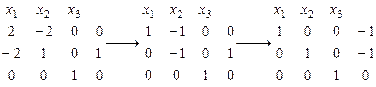
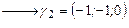Наконец, вектор 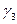является решением системы

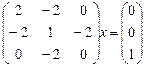
Преобразуем эту систему уравнений методом Гаусса

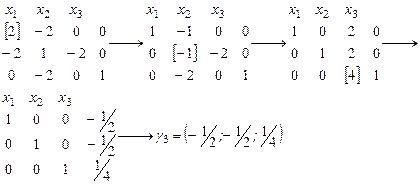Теорема. Если матрица квадратичной формы 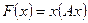удовлетворяет условию Якоби, то система векторов Якоби 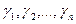матрицы является каноническим базисом квадратичной формы 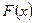, а выражение

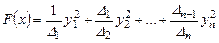
– ее каноническим видом в базисе 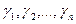. Наша форма в базисе Якоби имеет вид .

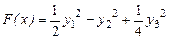Итак, в разных канонических базисах квадратичная форма имеет разный канонический вид, однако, положительный индекс (число положительных коэффициентов в каноническом виде) и отрицательный индекс остаются неизменными. У формы, рассмотренной в примерах 1 и 2 положительный индекс равен 2, а отрицательный индекс равен 1.