Квазилинейные уравнения 2-ого порядка бывают 3 видов:
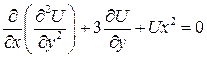 – третий порядок.
– третий порядок.
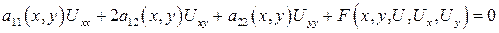
1) гиперболическая
2) параболическая
3) эллиптическая
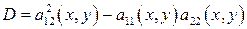 – дискриминант квазилинейного уравнения.
– дискриминант квазилинейного уравнения.
1) Если 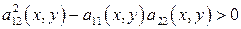 для любой точки
для любой точки 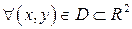 , то исходное уравнение принадлежит гиперболическому типу в области D.
, то исходное уравнение принадлежит гиперболическому типу в области D.
2) Если 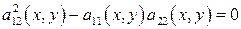 для любой точки
для любой точки 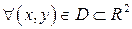 , то исходное уравнение принадлежит параболическому типу в области D.
, то исходное уравнение принадлежит параболическому типу в области D.
3) Если 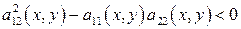 для любой точки
для любой точки 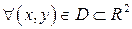 , то исходное уравнение принадлежит эллиптическому типу в области D.
, то исходное уравнение принадлежит эллиптическому типу в области D.
Приведение к каноническому виду уравнение 2-ого порядка с двумя независимыми переменными. Смысл приведения данного уравнения в частной производной к канонической форме (нормальной) состоит в том, что уравнение, приведенное к простому виду, т.ч. посл. решение данного уравнения сводится к простому (не сложн). Чтобы привести к каноническому виду квазилинейные дифференциальные уравнения в частной производной
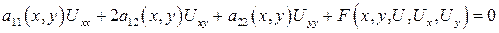
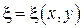 и
и 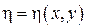 , чтобы исходное уравнение стало как можно проще.
, чтобы исходное уравнение стало как можно проще.
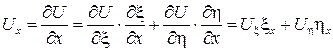
по теореме о замене переменных в функции многих переменных, аналогично 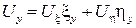 , тогда
, тогда
|
|
|
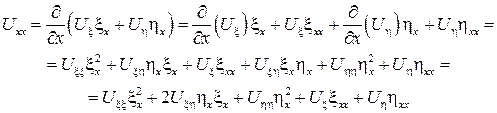
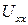 – 2 производная
– 2 производная
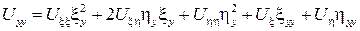
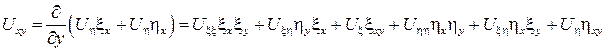
Подставим найденные производные в исходное уравнение. Получим уравнение:
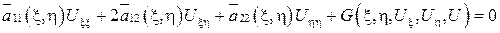 ,
,
где 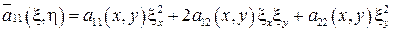 ,
,
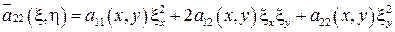 ,
,
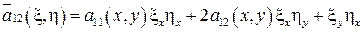 .
.
На самом деле в следующий раз мы покажем, что если исходное уравнение гиперболическое, то замену переменных 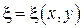 и
и 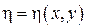 можно выбрать так, что
можно выбрать так, что 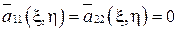 , а
, а 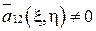 и тогда канонический вид гиперболического уравнения будет:
и тогда канонический вид гиперболического уравнения будет:
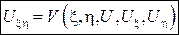
2) Если исходное уравнение параболическое, то замену переменных 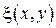 и
и 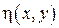 можно выбрать так, что либо
можно выбрать так, что либо 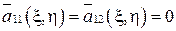 , а
, а 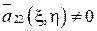 , либо
, либо 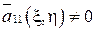 , а
, а 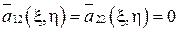 и канонический вид параболического уравнения будет
и канонический вид параболического уравнения будет
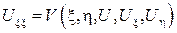
3) Если уравнение эллиптическое, то ξ и η можно выбрать так, что 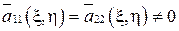 , а
, а 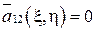 и канонический вид
и канонический вид
 2015-03-07
2015-03-07 3454
3454
