2015-06-24
4449
Если известны координаты векторов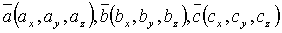 
, то смешанное произведение находится по формуле:
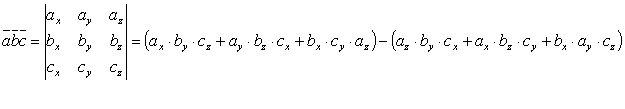
Пример: Вычислить смешанное произведение векторов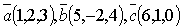 
.
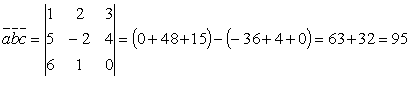
Свойства смешанного произведения:
1. Смешанное произведение не меняется при циклической перестановке его сомножителей: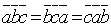 
.
Циклическая перестановка - порядок сомножителей не меняется, за исключением того, когда последняя буква встает в начало. То есть, с всегда идет после b (для данного произведения), а перед b. Сомножители переставляются как бы по кругу.
2. При перестановке двух соседних сомножителей смешанное произведение меняет свой знак на противоположный:
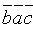
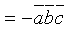(b и а меняются, с остается на месте.)
3. Если смешанное произведение равно нулю, то векторы a, b, c – компланарны.
(aхb) . c = 0
* Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости.
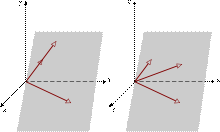
Геометрический смысл смешанного произведения:
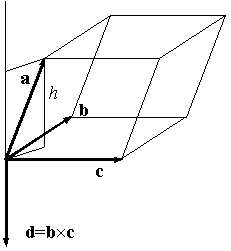
Смешанное произведение трех векторов равно объему параллелепипеда, построенного на приведенному к общему началу векторах, взятому со знаком плюс, если тройка abc правая, и со знаком минус, если тройка abc левая:
|
|
|
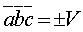
Доказательство:
Пусть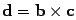 
. Нам известно, что «площадь параллеллограмма, сторонами которого служат векторы b и c, равна модулю их векторного произведения» (теорема). Отсюда 
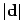равен площади 
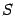параллелограмма, сторонами которого служат векторы b, c (Рис. 1)
Рис. 1:
