Если векторы заданы в прямоугольной декартовой системе координат своими координатами, то
1) при сложении двух и большего числа векторов их одноименные координаты складываются, т.е. если 
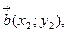 то
то 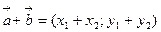 ;
;
2) при вычитании векторов их одноименные координаты вычитаются, т.е. если 
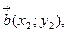 то
то 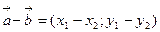 ;
;
3) при умножении вектора на число каждая координата вектора умножается на это число, т.е. если 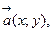 то
то 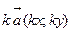
Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки на плоскости А(х 1; y 1), B(x 2; y 2), то
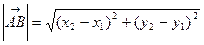 .
.
Если точка М(х; у) делит отрезок АВ в соотношении l/m, то координаты этой точки определяются как: 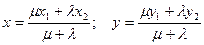
В частном случае координаты середины отрезка находятся как: 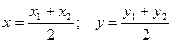
Скалярным произведением двух ненулевыхвекторов 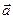 и
и 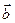 называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.
называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.
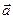 ×
× 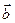 = ï
= ï 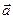 ï·ï
ï·ï 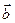 ï· cosj, где j - угол между векторами
ï· cosj, где j - угол между векторами 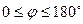 . Углом между векторами называется угол между их направлениями.
. Углом между векторами называется угол между их направлениями.
Пример. Найти скалярное произведение (3 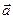 -2
-2 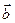 )×(5
)×(5 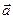 -6
-6 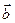 ), если
), если 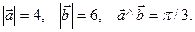
|
|
|
15 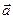 ×
× 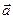 - 18
- 18 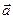 ×
× 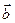 - 10
- 10 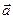 ×
× 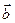 + 12
+ 12 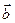 ×
× 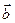 = 15
= 15 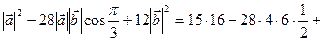 12×36 =
12×36 =
= 240 – 336 + 432 = 672 – 336 = 336.
 2015-06-24
2015-06-24 11274
11274








