Наименование занятия: Операции над векторами
Цель занятия: Научиться выполнять действия с векторами
Подготовка к занятию: Повторить теоретический материал по теме «Векторы. Операции над векторами»
Литература:
- Григорьев В.П., Дубинский Ю.А. «Элементы высшей математики», 2008г.
- Дадаян А.А. «Математика», 2004г.
Задание на занятие:
- Даны векторы
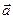 и
и 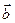 . Построить векторы
. Построить векторы 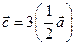 ,
, 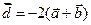 .
. - Найти координаты векторов
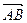 ,
, 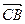 ,
, 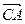 , если А (2; 3), В (-1; -3), С (-7; 5).
, если А (2; 3), В (-1; -3), С (-7; 5). - Даны векторы
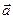 = (-2; 4) и
= (-2; 4) и 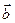 = (3; 1). Найти:
= (3; 1). Найти: 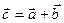 ,
, 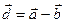 ,
, 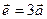 ,
, 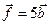 .
. - Найти длину вектора
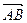 , если А (5; 2), В (8; -2).
, если А (5; 2), В (8; -2). - Дан треугольник с вершинами А (7; 7), В (4; 3), С (3; 4). Найти его периметр.
- Отрезок АВ задан точками А (2; 3), В (10; 11). Найти координаты точки С, если известно, что
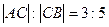 .
. - Найти длину медианы АМ треугольника с вершинами А (7; -4), В (-1; 8), С (-12; -1).
- Найти скалярное произведение векторов
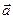 = (5; 7) и
= (5; 7) и 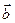 = (4; 3).
= (4; 3). - Найти угол между векторами
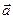 = (4; 0) и
= (4; 0) и 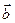 = (2; -2).
= (2; -2). - Найти углы треугольника с вершинами А (6; 7), В (3; 3), С (1; -5).
Порядок проведения занятия:
- Получить допуск к работе
- Выполнить задания
- Ответить на контрольные вопросы.
Содержание отчета:
- Наименование, цель занятия, задание;
- Выполненное задание;
- Ответы на контрольные вопросы.
Контрольные вопросы для зачета:
- Что называется вектором? Длиной вектора?
- Как сложить два вектора?
- Как найти разность двух векторов?
- Как умножить вектор на число?
- Как найти координаты вектора, заданного двумя точками?
- Как найти длину вектора, заданного двумя точками?
- Как найти длину вектора, заданного своими координатами?
- Как вычисляется скалярное произведение векторов, заданных своими координатами?
- Как найти угол между векторами?
ПРИЛОЖЕНИЕ
Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевойвектор – это вектор, начало и конец которого совпадают.
Длиной (модулем) вектора называется расстояние между началом и концом вектора.
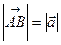
 2015-06-24
2015-06-24 1015
1015
