Th 1. Необходимое условие разложимости функции в степенной ряд

Пусть функция 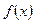в промежутке M разлагается в степенной ряд, тогда

1. Эта функция бесконечно дифференцируема в точке .
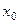2. Этот степенной ряд является рядом Тейлора.

□

1. Бесконечная дифференцируемость 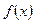в точке 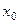вытекает из теоремы о почленном дифференцировании степенного ряда.

2. Предположим, что разложение функции в степенной ряд имеет вид (8). Из (8) при 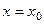получаем .

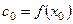Дифференцируя (8) почленно получим

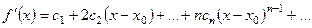. (11)

При .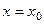

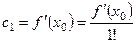Дифференцируя (11) почленно получим

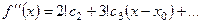(12)

При 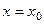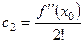и т.д.

Положим 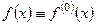, тогда получим формулу (9) для ряда Тейлора.

■