1. Краткая характеристика геометрического содержания курса математики начальной школы
2. Геометрические понятия в начальной школе
3. Задания на измерение и вычисление
4. Задания на построение.
5. Краткая характеристика геометрического содержания курса математики начальной школы
Одной из основных задач изучения геометрического содержания в курсе математики начальной школы является развитие пространственного воображения у ребенка, умения наблюдать, сравнивать, обобщать, анализировать и абстрагировать. Второй важной задачей является формирование у ребенка практических умений измерения и построения геометрических фигур с помощью циркуля, угольника и линейки. Задания на вычисления различных параметров геометрических фигур (длин отрезков, периметра и площади прямоугольника и квадрата) позволяют показать ребенку взаимосвязь количественных и пространственных характеристик объектов материального мира, а также показать еще одно приложение понятия «натуральное число» —"как результата измерения величин.
В соответствии с последней редакцией Обязательного минимума содержания образования по математике для начальных классов список изучаемых геометрических понятий значительно расширился по отношению к предыдущим вариантам стабильной программы. Общая тенденция геометризации курса школьной математики коснулась и начальных классов. В соответствии с этой тенденцией насыщение курса математики начальной школы геометрическим содержанием является перспективной линией развития математического образования начального звена.
Обязательный минимум содержания образования по математике содержит следующий перечень понятий геометрического характера:
Точка. Линии: прямые, кривые. Отрезок. Угол. Прямой угол. Многоугольники: треугольник, прямоугольник, квадрат. Вершины и стороны многоугольника. Окружность и круг. Куб. Шар.
Измерение длин.
Измерение площади. Вычисление площади прямоугольника.
По отношению к этому перечню, определяющему минимум содержания, сегодняшний традиционный учебник математики содержит намного больше геометрических понятий. Можно отметить, что сегодня стабильный учебник математики содержит даже больше геометрических понятий, чем многие альтернативные учебники развивающих систем.
Геометрические понятия в начальной школе
В 1 классе различные геометрические фигуры используются как материал для построения заданий на распознавание, сравнение, обобщение и классификацию. Цель этих заданий — формирование и развитие наблюдательности ребенка; формирование и развитие умения выделять существенные (важные) признаки предмета, умения сравнить два или несколько предметов, отмечая при этом сходные и различные признаки и свойства; умения сделать несложное обобщение на основе выделенных общих свойств предметов; умения распределять предметы на группы (классификация) в соответствии с выделенным признаком.
Такие задания являются основными для формирования и развития мыслительных операций (анализ, синтез, сравнение, классификация и др.), а также умения строить обоснованные (логические) рассуждения. Необходимость обучать детей всем этим умениям оговорена в Обязательном минимуме содержания образования для начальной школы в разделе «Требования к уровню подготовки выпускников начальных классов» (М., 2001).
Геометрические понятия, с которыми дети знакомятся в 1 классе:
Точка. Линия — кривая и прямая. Отрезок. Ломаная. Звенья ломаной. Вершина ломаной. Замкнутая и незамкнутая ломаная. Многоугольники. Треугольники и четырехугольники.
Точка — неопределяемое понятие геометрии. С точкой обычно знакомят методом показа — рисуют или прокалывают стержнем ручки в листочке бумаги. Считается, что точка не имеет ни длины, ни ширины, ни площади.
Линия — неопределяемое понятие геометрии. С линией знакомят методом показа — моделируют из шнура, или рисуют на доске или на листе бумаги.
Прямую линию удобно моделировать, сгибая любой лист бумаги — линия сгиба всегда прямая. Основное свойство прямой линии: прямая линия бесконечна.
Кривую линию удобно моделировать из шнура. Кривая линия также бесконечна (если она не замкнутая).
Ломаную линию удобно моделировать, используя счетные палочки или складной металлический метр. Ломаная линия содержит конечное число звеньев. Звено ломаной — отрезок. Точки соединения концов звеньев называют — вершинами ломаной. Звенья ломаной должны быть соединены последовательно.
Например:

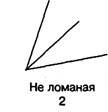
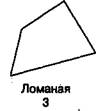
В программе 1 класса линии рассматривают только на плоскости.
Основные взаимоотношения точки и прямой или кривой линии, с которыми знакомятся дети в 1 классе:
1. Через одну точку можно провести множество прямых.
2. Через одну точку можно провести множество кривых.
3. Через две точки можно провести только одну прямую.
4. Через две точки можно провести множество кривых.
Отрезок — часть прямой, заключенная между двумя точками.
Отрезок имеет определенную длину, которую можно измерить.
Линейка — инструмент для измерения длин отрезков.
Ломаная и кривая линии могут быть замкнутыми и незамкнутыми. На рисунке ломаная 1 — незамкнутая, ломаная 3 — замкнутая.
Замкнутая ломаная на плоскости ограничивает многоугольник.
Многоугольник — плоская фигура, ограниченная замкнутой ломаной.
Треугольник — ограничен ломаной из трех звеньев. Соответственно имеет три стороны и три вершины.
Четырехугольник — ограничен ломаной из четырех звеньев. Соответственно имеет четыре стороны и четыре вершины.
Геометрические понятия, с которыми дети знакомятся во 2 классе: Длина ломаной. Прямой угол. Непрямой угол. Прямоугольник. Квадрат.
Длина ломаной — сумма длин звеньев ломаной. Для нахождения длины ломаной следует измерить длину каждого звена и результаты сложить.
Прямой угол — это угол, который по определению содержит 90°. Поскольку в начальной школе при обучении по стабильной программе дети не знакомятся с градусной мерой углов, понятие прямого угла дается методом показа:
Для получения модели прямого угла дети используют лист бумаги, сгибая его соответствующим образом:
Прямой угол
Методом проб дети учатся находить прямой угол среди рисунков других углов и на различных геометрических фигурах: прикладывают к ним свою модель, выделяя углы, с ней совпадающие. Модель прямого угла служит средством проверки такого выбора. В дальнейшем бумажная модель прямого угла заменяется угольником, который является основным инструментом для распознавания и построения прямых углов.
Прямоугольник — четырехугольник, у которого все углы прямые. Основное свойство прямоугольника: противолежащие стороны прямоугольника имеют равные длины.
Это свойство дети определяют опытным путем: перегибают бумажные модели прямоугольников, совмещая противолежащие стороны.
При невозможности применить этот метод, его заменяют измерением длин противолежащих сторон.
Используя это свойство, дети должны уметь чертить прямоугольник по известным длинам двух его сторон, понимая, что две другие стороны имеют такие же длины, а углы его — прямые.

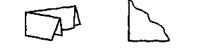
Квадрат — прямоугольник, у которого все стороны равны.
Используя это определение, дети должны уметь чертить квадрат по известной длине одной стороны, понимая, что все остальные стороны квадрата имеют такую же длину, а углы его — прямые.
Геометрические понятия, с которыми знакомятся в 3 классе:
Периметр многоугольника. Площадь прямоугольника. Круг. Окружность. Радиус. Диаметр. Треугольники равносторонние, равнобедренные и разносторонние.
В 3 классе дети знакомятся с обозначением фигур заглавными латинскими буквами.
Чтобы назвать отрезок, обозначают точки, которые являются его концами.
Например: отрезок М N. М--------------------------N
Чтобы назвать многоугольник, обозначают буквами его вершины. Например: квадрат АВСD.

Чтобы назвать ломаную, также обозначают буквами ее вершины. Например: ломаная РКЕB.
Периметр многоугольника — сумма длин всех его сторон. Для нахождения периметра многоугольника измеряют длины его сторон и складывают полученные результаты.
Периметр квадрата находят умножением на 4 длины его стороны, поскольку стороны квадрата имеют равные длины.
Периметр прямоугольника находят, складывая суммы длин двух его непротиволежащих сторон, и умножая результат на 2.
Площадь плоской фигуры измеряется количеством стандартных мер площади, укладывающихся внутрь фигуры. Стандартные меры площади: мм²; см²; дм²; м²; км².
В 3 классе дети знакомятся с см².
Инструмент для определения площади всех фигур — палетка.
Палетка — лист кальки (или прозрачного пластика), на который нанесена сетка квадратов размером 1 см х 1 см. Для измерения площади фигуры с помощью палетки, ее накладывают на фигуру

и подсчитывают примерное число полных квадратных сантиметров в измеряемой фигуре. Для получения приближенного значения площади фигуры, число неполных квадратных сантиметров обычно рекомендуется разделить на 2.
Способ нахождения площади прямоугольника: Чтобы вычислить площадь прямоугольника, измеряют его длину и ширину (в одинаковых единицах) и находят произведение полученных чисел.
Например:
От прямоугольного листа со сторонами 5 см и 3 см отрезали полоску со сторонами 3 см и 1 см. Найди площадь оставшейся части.
Решение:
1. Найдем площадь данного листа: 5 см • 3 см = 15 см².
2. Найдем площадь полоски: 3 см • 1 см = 3 см².
3. Найдем разницу площадей: 15 см² - 3 см² =12 см². Используя чертеж, данную задачу можно решить другим способом:
Зсм
Анализ рисунка сразу показывает, что оставшаяся часть имеет площадь: 3 см • 4 см = 12 см².
Окружность и круг образованы замкнутой кривой линией. Круг — часть плоскости, ограниченная окружностью. Граница круга — окружность.
Поскольку в начальных классах не знакомят детей с классическим определением окружности (множество точек, равноудаленных от центра), знакомство с окружностью проводят методом показа, связывая его с непосредственной практической деятельностью по вычерчиванию окружности при помощи циркуля. Замкнутая кривая линия, которую рисует грифель циркуля — это окружность. Окружность (круг) имеет центр: точка О -центр окружности (круга).
Радиус окружности — отрезок, соединяющий центр окружности с какой-нибудь ее точкой. Например: ОМ — радиус окружности (круга). Основное свойство радиусов одной окружности: Радиусы одной окружности (круга) равны.
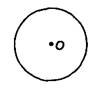
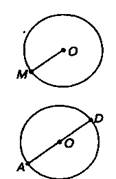
Диаметр окружности (круга) — отрезок, проходящий через центр окружности (круга) и соединяющий две любые ее точки.
Например: диаметр АО.
Основное свойство диаметров одной окружности (круга): Диаметры одной окружности (круга) равны.
Отношения между радиусом и диаметром одной окружности (круга): Диаметр равен двум радиусам.
Треугольники, имеющие стороны разной длины, называют разносторонними.
Треугольники, у которых равны две стороны, называют равнобедренными.
Среди равнобедренных треугольников есть такие, у которых равны все три стороны. Эти треугольники называют равносторонними.
Геометрические понятия, с которыми дети знакомятся в 4 классе:
Диагонали прямоугольника. Свойства диагоналей прямоугольника.
Луч. Числовой луч.
Угол. Элементы угла. Прямой, острый и тупой угол. Треугольники остроугольные, прямоугольные и тупоугольные.
Диагональ многоугольника — отрезок, соединяющий противолежащие вершины многоугольника.
С диагоналями прямоугольника детей знакомят методом показа:
Например:
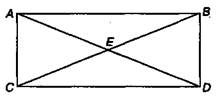
Отрезки АЕ и С — диагонали прямоугольника АВDС.
Точка Е — точка пересечения диагоналей.
Основные свойства диагоналей прямоугольника:
Диагонали АD и В С имеют равные длины.
Отрезки, получаемые при пересечении диагоналей прямоугольника, равны.
Данные свойства определяются эмпирическим (опытным) путем — измерением длин соответствующих отрезков.
Поскольку квадрат является прямоугольником, то его диагонали обладают теми же свойствами. Кроме того, диагонали квадрата пересекаются под прямым углом.
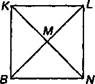
Например:
Непосредственное измерение углов с помощью угольника показывает, что углы, получающиеся при пересечении диагоналей квадрата, прямые.
Луч — часть прямой, ограниченная с одной стороны.
Луч имеет начало, но не имеет конца.
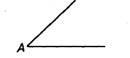
Изображение луча:
Точка А — начало луча.
В математике луч обычно обозначается двумя буквами, например: луч АС. Такая запись обозначает, что луч имеет началом точку А и «идет» в сторону, обозначенную буквой С:
Числовой луч — луч, на котором точками обозначены натуральные числа. Расстояние между точками равно 1 единице измерения (единичный отрезок), которая задается условно. Чаще всего это 1 или 2 клетки.
Каждой точке ставится в соответствие число, начиная с числа 1. Началу луча ставится в соответствие число 0.
Числовой луч играет большую роль при иллюстрации понятия натуральный ряд чисел, позволяет сравнивать натуральные числа, ориентируясь на их расположение на числовом луче, позволяет выполнять приемы присчитывания и отсчитывания по частям с опорой на числовой луч. В связи с этим некоторые альтернативные учебники (Н.Б. Истомина) знакомят детей с этим понятием еще в 1 классе.
Другая роль числового луча состоит в том, что используя это понятие, можно познакомить детей с прямоугольной системой координат (числовой или координатный угол), отрицательными числами (числовая прямая).
Например:
Объясни с помощью числового луча, в какую сторону от точки, соответствующей точке 8, надо двигаться, чтобы найти все числа, которые меньше числа 8, и те числа, которые больше, чем 8.


Ответ: Чтобы найти все числа, которые меньше, чем 8, нужно двигаться влево от числа 8. Чтобы найти числа, которые больше, чем число 8, нужно двигаться от него вправо.
Угол — это фигура, образованная двумя лучами, имеющими общее начало.
Стороны угла — это лучи, образующие угол.
Вершина угла — это общее начало лучей, образующих угол.
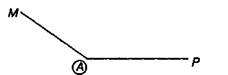
Обозначение угла: угол может быть назван по его вершине -угол М; угол может быть назван тремя буквами — угол МАР, при этом буква, стоящая в вершине угла, должна быть средней.
Например:
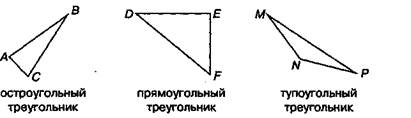
Остроугольный треугольник — треугольник, все углы которого острые.
Прямоугольный треугольник имеет один прямой угол. Тупоугольный треугольник имеет один тупой угол. Например:
В треугольнике не может быть более одного прямого угла.
В треугольнике не может быть более одного тупого угла.
Равносторонний треугольник может быть только остроугольным.
Прямоугольный и тупоугольный треугольники могут быть равнобедренными.
Разносторонними могут быть и остроугольный, и прямоугольный, и тупоугольный треугольники.
 2015-06-26
2015-06-26 50599
50599