5. С какими областями научных знаний непосредственно связана методика преподавания математики в начальных классах?
б. Приведите примеры использования в методике преподавания математики законов марксистско-ленинской теории познания.
7. В чем с методической точки зрения состоит различие между математикой наукой и математикой — предметом изучения в начальных классах?
8. Методика преподавания любой дисциплины опирается на психолого-педагогические исследования. Характерны ли в этом плане какие-либо особенности для методики преподавания математики?
9. Раскройте специфику применения логики в преподавании математики в начальных классах.
Приведем сначала строгое математическое доказательство равенства 5+8= 13:
5+8=5+ (5+3) закон ассоциативности
= (54-5) +3) сложения
=104-3
= 13.
На предматематическом уровне оно может выглядеть так: 5+8=
= 5+5+3=10 + З = 13.
Различие между приведенными доказательствами состоит не только в том, что в последнем нет скобок. даже если бы здесь использовались скобки, это не означало бы применения некоторого закона. То, что в математике формулируется в виде закона, в данном случае закона ассоциативности сложения, на предматематическом уровне считается интуитивно истинным. Это свойство, обоснованное с помощью интуиции, выделяется в дальнейшем обучении в соответствующий закон.
Предматематика это не «детская математика». На предматематическом уровне изучаются некоторые понятия и темы школьного курса математики и в средних, и в старших классах. Этот уровень часто является достаточным и для научно-популярной литературы. Что же касается обучения математике в начальных классах школы, то оно осуществляется исключительно на предматематическом уровне. Поэтому правомерно говорить о том, что в начальной школе учащиеся получают «предматематическую» подготовку. Она позволяет им в последующих классах перейти к изучению систематических курсов алгебры, геометрии и начал анализа.
Концепция предматематики хорошо согласуется с реальным процессом обучения в начальных классах, поэтому предматематику естественно рассматривать как основу такого обучения. На этой основе в обучении легче реализовать дидактические принципы (научности, наглядности и др.), использовать арсенал средств и методов обучения математике. Необходимо, однако, отметить, что предматематика до сих пор в полном объеме не разработана.
4. ЦЕЛИ НАЧАЛЬНОГО ОБУЧЕНИЯ МАТЕМАТИКЕ
Цели обучения математике в начальных классах отвечают общим целям обучения в средней школе в соответствии с требованиями реформы. Средняя общеобразовательная школа призвана готовить высокообразованных, всесторонне развитых, активных членов социалистического общества, способных к творческому труду. Большинство профессий требует определенной математической подготовки. В современных условиях математические знания, владение характерными для математики методами и специфическим языком обязательный элемент общей культуры. Изучение математики способствует формировании научного мировоззрения учащихся, воспитанию трудолюбия, честности, дисциплинированности и других моральных качеств. Навыки мыслительной деятельности. приобретаемые учащимися в процессе правильно организованного обучения математике, готов к упорному труду, преодолению трудностей будут нужны им в будущем независимо от того, какую профессию изберет каждый из них после окончания школы.
Таким образом, из сказанного видно, что обучение математике в школе, в том числе в начальных классах, преследует достижение четырех взаимосвязанных целей: общеобразовательных овладение
учащимися определенным объемом математических знаний, умений и навыков в соответствии с программой; воспитательных формирование марксистско-ленинского мировоззрения, важнейших моральных качеств, готовности к труду; развивающих — развитие логических структур и математического стиля мышления; практических — формирование умения применять математические знания в конкретных ситуациях, при решении практических задач.
Изучение математики в У—Х1 классах базируется на математической (а точнее, предматематической) подготовке, полученной учащимися при обучении в начальных классах.
Согласно Типовой программе МП СССР по ‘математике для Т—IУ классов, школьники, оканчивающие IУ класс, должны знать:
таблицу сложения (однозначных чисел) и соответствующие случаи вычитания; таблицу умножения однозначных чисел и соответствующие случаи деления; названия и обозначения единиц важнейших величин—длины (км, м, дм, см, мм), массы (кг, г), площади (м2, дм2, см2), скорости (км/ч, м/с), времени (ч, мин, с).
Школьники, оканчивающие IУ класс, должны уметь: читать, записывать и сравнивать числа в пределах миллиона; выполнять несложные устные вычисления; производить письменные вычисления (сложение и вычитание чисел в пределах миллиона, умножение двузначного и трехзначного чисел на однозначное, двузначное и трехзначное числа, деление трех-,.четырех-, пятизначного числа на однозначное и на двузначное числа); называть компоненты арифметических действий и читать простейшие числовые выражения (сумму, разность, произведение, частное); вычислять значение числового выражения (в том числе выражения со скобками), содержащего 3—4 арифметических действия, с помощью правил порядка выполнения действий и свойств арифметических действий; решать простые текстовые арифметические задачи, раскрывающие смысл каждого действия и смысл отношений «меньше на», больше на», «меньше в», больше в решать составные задачи и задачи, требующие знания зависимости между важнейшими величинами (скоростью, временем и расстоянием при равномерном прямолинейном движении, ценой, количеством и стоимостью товара, площадью прямоугольника и длинами его смежных сторон и др.); распознавать и изображать (с помощью циркуля, угольника и линейки) простейшие геометрические фигуры (точку, отрезок, ломаную, окружность, круг, прямоугольник); измерять длину отрезка, длину ломаной; строить отрезок данной длины; вычислять периметр и площадь прямоугольника.
Перечисленными знаниями и умениями должны овладеть все учащиеся IУ класса. Исходя из этого заданного результата обучения, знания и умения «распределяются» по классам, годам обучения в соответствии с программой. Многие из перечисленных знаний и умений формируются постепенно в течение четырех лет обучения. Например, умение читать, записывать и сравнивать числа в пределах миллиона ученик приобретает начиная с первого класса. Параллельно с этим учащиеся овладевают умениями устных и письменных вычислений, решения арифметических задач, В процессе начального обучения математике у учащихся формируются также некоторые черты математического и логического стиля мышления.
5. СОДЕРЖАНИЕ КУРСА МАТЕМАТИКИ В НАЧАЛЬНЫХ КЛАССАХ
Общие положения. Содержание начального курса математики определяется целями обучения. С этой точки зрения рассмотрим его важнейшие элементы. Курс математики для младших школьников должен обеспечивать преемственность в изучении математики в средних и старших классах. Это может достигаться по следующим направлениям.
1. Некоторые математические знания и умения (с учетом особенностей механизма запоминания, характерных для детей младшего школьного возраста) могут быть качественно усвоены именно в начальных классах. Здесь в первую очередь имеются в виду табличные случаи сложения (вычитания), умножения (деления), а также умения, в основе которых лежат несложные алгоритмы.
Одним из важнейших классов алгоритмизируемых умений являются устные и письменные вычисления. Отработанные в младшем школьном возрасте навыки вычислений на множестве натуральных чисел позволяют учащимся в дальнейшем достаточно легко овладеть более сложными алгоритмами вычислений на множестве рациональных и действительных чисел: Поэтому приемы устных и письменных вычислений (сложение, вычитание, умножение и деление) являются естественными элементами программы по математике для начальных классов.
2. С некоторыми базовыми математическими понятиями среднёй школы учащихся начальных классов можно легко ознакомить на пропедевтическом уровне, используя житейский опыт учащихся, их наглядно-образные представления.
Так, манипулирование множествами хорошо известных учащимся предметов служит основой для формирования у них понятия числа, арифметической операции. Наблюдения за окружающим миром дают возможность выделить наиболее часто встречающиеся в действительности формы. Таким образом, целый ряд геометрических фигур становится предметом изучения в начальной школе.
З. Важным условием полноценного обучения математике является формирование у учащихся навыков математической деятельность.
В методике под термином «математическая деятельность» понимают деятельность, ходню по своей сути с математическим познанием. Выделяют три вида математической деятельности, выступающих в органическом единстве: математическую организацию эмпирического
материал а, логическую организацию математического материала, применение математических теорий.
В начальных классах возможно целенап5Пвленное формирование у учащихся навыков математической организации эмпирического материала. Однако при этом учебный материал должен удовлетворять определенным условиям.
Существуют два подхода к формированию математических понятий: генетический и аксиоматический. Аксиоматический подход предполагает, в частности, высокий уровень владения учащимися языком, на котором ведется преподавание. Естественно, что языковая культура младших школьников только формируется, поэтому аксиоматический подход в начальных классах нереален.
Генетический подход заключается в том, что житейские, эмпирические понятия и представления учащихся «переводятся» на язык математики и закрепляются в форме математических понятий. Такой процесс называется математизацией эмпирического материала (математизацией) и соответствует возможностям младших школьников.
В практике обучения организация деятельности учащихся по математизации и управление ею осуществляются учителем. Однако при рациональной методике учащиеся в состоянии не только усваивать результаты математизации, но в накапливать опыт ее осуществления. Понятно, что такая методика требует, чтобы вопросы, включенные в программу по математике, имели многочисленные (исходя из жизненного опыта детей) интерпретации в реальном мире. Исходя из этих позиций, в программу для начальной школы может быть включен весьма необычный с точки зрения традиций этой школы математический материал. Примером может служить содержание программы, по которой обучались воспитанники одного из детских садов Бельгии (Ф. Папи, Ж. Папи. Дети и графы.— М., 1974), математический материал для занятий с детьми 6—10 лет, разработанный Р. Ф. Соболевским (Логические и математические игры.— Мн., 1977).
4. Программа по математике должна предусматривать также овладение учащимися математическим языком — средством математизации. Математический язык учащихся начальных классов с синтаксической точки зрения не должен отличаться от языка старшеклассников. Например, предложение •+••=з («к одному яблоку прибавить два яблока...») не является математическим ни для математика, ни для старшеклассника, ни для ученика 1 класса. Что же касается смыслового значения математических терминов, знаков, используемых в младших классах, то оно, конечно, беднее соответствующих языковых средств учащихся старших классов, однако не противоречит ему.
Остановимся на более характерных особенностях действующей программы по математике для начальной школы. В содержании программы можно выделить арифметический, геометрический и алгебраический материал, а также материал, связанный с изучением величин. Такое разделение условно, поскольку в младших классах в отличие от средних и старших ни арифметика, ни геометрия, ни алгебра не являются систематическими курсами. Соответствующие понятия не образуют строгой логической системы.
Арифметический материал. Этот материал занимает в программе центральное место. Целью его изучения является знакомство учащихся с понятием числа — целыми неотрицательными числами и обыкновенными дробями. В средних и старших классах это важнейшее понятие последовательно расширяется.
Из курса математики для факультета педагогики и методики начального обучения (в дальнейшем для краткости будем называть его вузовским курсом математики) известно, что существуют два подхода к определению целых недельных чисел количественный и аксиоматический. В начальных классах реален первый из названных. Понятие натурального числа вводится через рассмотрение свойств конечных множеств. Множества служат основой для формирования у учащихся представлений об упорядоченности целых неотрицательных чисел, арифметических операциях.
Важное место в курсе математики начальных классов занимают законы арифметических операций: коммутативности и ассоциативности сложения и умножения, дистрибутивности умножения относительно сложения.
Арифметический материал изучается концентрически. Поскольку он составляет основу программы по математике, то элементы геометрии и алгебры распределены по соответствующим концентрам. Необходимость знакомства учащихся с понятием числа по концентрам выявляется при логико-дидактическом анализе арифметического материала. В нем можно выделить два основных элемента — нумерацию и арифметические операции.
Рассмотрим сначала логическую последовательность изучения нумерации целых неотрицательных чисел. При этом будем исходить из того, что нумерация изучается в десятичной позиционной системе счисления.
1. Нумерация чисел первого десятка (0, 1 9). Изучается «алфавит» десятичной системы счисления — написание и название цифр.
2. Нумерация чисел второго десятка (11, 12 19). Названия
этих чисел образуются по особому правилу: 11 «один-на-дцать»,
12 — «две-на-дцать»,..., 19 «девять-на-дцать». При изучении
нумерации используются понятие «десяток» и знания, полученные
в концентре 1.
3. Нумерация круглых десятков (20, 30 90). Названия этих чисел имеют сходство: «два-дцать», «три-дцать» (вместе с тем <сорок», «девяносто»). Для их нумерации используются понятие «Десяток» и знания, полученные в концентре 1.
4 Нумерация остальных двузначных чисел (21, 22 99). Названия этих чисел образуются из двух слов — сначала называется число десятков, а затем число единиц. Для их нумерации используются знания, полученные в концентрах 1 и 3.
Порядок изучения концентров 1, 3, 4 должен строго соблюдаться
— сначала 1, затем 3, затем 4. Изучать концентры 2 и З можно в разной последовательности.
5. Нумерация круглых сотен (100, 200 900). Названия этих чисел имеют сходство: «сто», «две-сти», «три-ста» «девять-сот». Для изучения нумерации этих чисел используются понятие «сотня» (разряд сотен) и знания, полученные в концентре 1.
6. Нумерация остальных трехзначных чисел (101, 102,... 213,
999). Здесь используются знания, полученные в концентрах 1—5.
7. Нумерация чисел класса тысяч (1000—999 999). Вводятся понятия «класс» и «тысяча». Обобщаются знания о разрядах. Используются знания, полученные во всех предыдущих концентрах.
8. Нумерация чисел свыше 999 999. Сообщаются названия новых классов (миллион, миллиард, триллион и т. д.). Устная и письменная,
нумерации этих чисел производятся по уже известным правилам.
Итак, логика изучения нумерации целых неотрицательных чисел определена. Однако учащиеся должны усваивать нумерацию в органической связи с изучением арифметических операций. Поэтому
с методической точки зрения концентры 1—8 далеко не равноценны. В самом деле, при изучении нумерации чисел в пределах десяти, например, учащиеся знакомятся с операцией сложения на множестве чисел первого десятка. Процесс усвоения табличного сложения (в пределах 10) весьма сложный и длительный. Однако знание учащимися таблицы сложения существенно облегчает изучение операции сложения в концентрах З и 5: эти суммы — 20 + 30, 200 + + 300 рассматриваются как 2 дес. + З дес., 2 сот. + З сот., т. е. как суммы однозначных чисел. Поэтому на изучение нумерации круглых десятков и сотен отводятся считанные уроки.1
Таким образом, в программе по математике выделяются более крупные концентры, чем 1—8.
Рассмотрим несколько примеров концентрического построения программ по математике для начальной школы.
В дореволюционной программе по математике для начальной школы (конец ХIХ в.) выделялись три концентра: числа первого десятка, числа первой сотни, многозначные числа. В первом кон- центре усваивалась нумерация и смысл всех четырех арифметических операций. Запоминались табличные случаи сложения и умножения (вычитания и деления) в пределах десяти. Во втором концентре учащиеся получали знания о нумерации чисел в пределах ста. Здесь же усваивались таблицы сложения и умножения, приемы устного внетабличного сложения и вычитания, умножения и деления в пределах ста. В третьем — вместе с нумерацией многозначных чисел (больших ста, меньших миллиарда) изучались приемы письменного сложения, вычитания, умножения (в столбик) и деления (углом).
В советской послевоенной программе (1945 г.) учебный материал по математике был распределен по пяти концентрам: числа первого десятка, числа второго десятка, числа в пределах ста, тысячи, многозначные числа. В первом концентре параллельно с нумерацией изучались табличные случаи сложения и соответствующие случаи вычитания в пределах десяти. Во втором концентре завершалось усвоение учащимися таблицы сложения и начиналась работа над таблицей умножения и соответствующими случаями деления в пределах 20. В третьем концентре завершалось изучение таблицы умножения. Отрабатывались приемы устного сложения и вычитания, умножения и деления в пределах ста, В четвертом концентре учащиеся усваивали приемы письменного выполнения всех четырех арифметических действий. В последнем концентре эти приемы отрабатывались при выполнении действий над многозначными числами (до триллиона).
В программе, утвержденной МП РСФСР в 1968 г., арифметический материал группировался по четырем концентрам: «десяток», «Сотня», «Тысяча», «Многозначные числа».
В концентре «десяток» учащиеся усваивали табличные случаи сложения (соответствующие случаи вычитания); в концентре «Сотня» таблицу сложения в целом, таблицу умножения (соответствующие случаи деления), приемы устного сложения, вычитания, умножения и деления в пределах ста; в концентре «Тысяча»
приемы письменного сложения и вычитания; в концентре «Многозначвые числа» -—- приемы письменного умножения и деления на множестве чисел до миллиарда.
В программе для четырехлетней начальной школы, утвержденной МП РСФСР в 1986 г., по существу выделено пять концентров: числа первого десятка, числа второго десятка, числа в пределах ста, числа в пределах тысячи, многозначные числа.
В первом концентре параллельно с изучением нумерации раскрывается смысл операций сложения и вычитания, учащиеся запоминают таблицу сложения и соответствующие случаи вычитания в пределах десяти. Во втором концентре завершается усвоение учащимися таблицы сложения, в третьем отрабатываются приемы устного сложения и вычитания. Наряду с этим учащиеся должны овладеть приемами письменного выполнения этих действий (в столбик). Вычисления в столбик они выполняют в наиболее сложных случаях. Здесь же учащиеся знакомятся с умножением и делением, усваивают таблицу умножения, приемы устного внетабличного умножения и деления. При изучении чисел в пределах тысячи вводятся приемы письменного умножения (в столбик) и деления (углом). В последнем концентре навыки устных и письменных вычислений обобщаются для действий над многозначными числами (до миллиона).
Несмотря на различное построение рассмотренных программ, нумерация в каждой из них изучается в соответствии с выделенной выше последовательностью этапов 1 —8. Различие программ обусловлено разными позициями авторов относительно изучения арифметических операций. Так, составители дореволюционной программы и программы 1945 г. считали необходимым начинать изучение всех четырех арифметических действий уже в концентре «десяток»; в программе 1986 г. в отличие от всех предыдущих предусмотрено письменное (в столбик) сложение и вычитание уже на множестве чисел первой сотни. Мы не будем здесь обсуждать достоинства и недостатки рассмотрены программ. Отметим только, что многие вопросы, касающиеся арифметического содержания программы iо математике, еще не нашли в методике полного решения. Таким образом, процесс совершенствования программы по математике для начальных классов продолжается.
Геометрический, алгебраический материал и величины, изучаемые в начальных классах, имеют важное образовательное значение. Однако при включении этого материала в программу по математике исходят из того, что он должен быть тесно связан с арифметикой. Например, изучение многоугольников начинается тогда, когда учащиеся знакомятся с числами первого десятка: наряду с различными множествами бытовых предметов для иллюстрации используются геометрические фигуры. Так, число 4 ставится в соответствие множествам, содержащим 4 яблока, 4 автомашины и т. д., и четырехугольнику фигуре, имеющей 4 стороны, 4 вершины, 4 угла. С понятием длины учащиеся знакомится при изучении темы «десяток». Линейка при этом используется для иллюстрации упорядоченности натуральных чисел, операций сложения и вычитания. дециметр, например, интерпретируется как десяток (счетная единица), метр
как сотня.
Геометрический материал. Пространственные представления формируются у детей в раннем возрасте, задолго до школы, что позволяет начать уже с первого класса математическое описание некоторых основных геометрических фигур. Слово «основные» имеет здесь совсем не тот смысл, который вкладывается в него в старших классах при изучении систематического курса геометрии. Там основными называют неопределяемые понятия, которые вместе с аксиомами составляют базу аксиоматической теории. Употребляя выражение «основные понятия» по отношению к начальному курсу математики, имеют в виду, что соответствующие геометрические фигуры
широко и ярко представлены в окружающем мире. К ним относятся:
прямая, точка, отрезок. угол, многоугольник (прямоугольник, квадрат), окружность и круг. Отметим, что к числу таких фигур было бы естественно отнести и прямоугольный параллелепипед, куб (эти фигуры до 60-х годов изучались в начальной школе).
Содержание и структура программы предполагают изучение геометрических понятий в тесной связи с арифметическим материалом, а также с изучением величин. Последнее достигается за счет того, что при знакомстве с геометрическими фигурами большое место отводится измерениям.
Кроме того, программой не предусмотрено раскрытие логических связей между геометрическими понятиями, поэтому от учащихся не требуется знания определений. Содержание понятий раскрывается через построение соответствующих геометрических фигур, эмпирическое исследование их моделей.
Тот факт, что ученик начальных классов усвоил то или иное геометрическое понятие, означает, что он, во-первых, может находить соответствующую геометрическую фигуру среди других фигур, вычленять ее из более сложных фигур, указывать реальные объекты,
имеющие соответствующую форму, во-вторых, умеет строить эту фигуру, в-третьих, может определять некоторые численные характеристики: количество углов, сторон, вершин, длину, радиус, периметр, площадь.
Важное место при изучении геометрических фигур играет знакомство учащихся с чертежными и измерительными инструментами:
линейкой, угольником, циркулем, рулеткой, палеткой.
Алгебраический материал. Основными алгебраическими понятиями, включенными в программу, являются переменная, выражение с переменной, уравнение. Пропедевтическое значение этих понятий невелико. При изучении систематического курса алгебры алгебраические понятия вводятся на качественно другой основе. В курс начальной школы включаются только те элементы алгебры и на таком уровне, который необходим для качественного усвоения учащимися арифметики целых неотрицательных чисел.
Уже при изучении чисел первого десятка у учащихся должно быть выработано представление об отношении порядка на множестве натуральных чисел. В связи с этим в систему упражнений включаются, например, такие задания: «Назови числа, которые можно подставить в «окошечко»: О 4, 7. О и т. д.> Позже, когда у учащихся формируются знания о связи между компонентами и результатами арифметических действий, могут использоваться более сложные упражнения: П + 4 7,7— П. 3,0.3. 8,12: П 2ит.д. По форме эти задания являются неравенствами с переменной, однако говорить об обучении учащихся начальных классов решению неравенств, очевидно, нельзя.
для того чтобы учащиеся запомнили таблицы сложения и умножения, используются следующие упражнения: 0+3=7, 5—О = 2, 6+0=8, 0. 3=24,5. 0=45,64:0=8, 0:7=6 и т. д. В последующем «окошки» заменяются буквами латинского алфавита. Уравнения учащиеся решают подбором, используя знания о связи между компонентами и результатами арифметических операций.
Буквенные обозначения широко применяются при отработке у школьников вычислительных навыков: ими обозначают термины
«слагаемое», «сумма», «разность», «множитель» и т. д. Примером может служить упражнение: Найти неизвестное число:
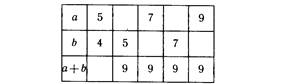
Особенности изучения математических понятий. Особенности развития мышления и речи учащихся начальных классов определяют требования к методике введения начальных математических понятий. Важнейшим из них является формирование математических понятий через рассмотрение реальных, житейских ситуаций, хорошо знакомых детям из повседневной жизни. Иначе говоря, каждому математическому понятию должна соответствовать система целесообразных текстовых содержательных задач. Эта особенность находит свое отражение в программе по математике: интенсивное обучение учащихся
решению содержательных задач предусмотрено с первых уроков математики проаммой определена последовательность знакомства учащихся сосновньтми типами задач. Например, с терминами «задача», «условие задачи», «вопрос задачи», «решение задачи» учащиеся знакомятся при изучении операций сложения и вычитания на множестве чисел первого десятка. Это дает возможность решить с учащимися целую систему задач. В частности, это могут быть задачи, в которых рассматриваются множества реальных объектов: стая птиц, группа мальчиков, флотилия кораблей, яблоки, лежащие в корзинке. Над каждым из этих множеств производится соответствующая операция: прилетает еще одна птица, прибегает еще один мальчик, подплывает еще один корабль, кладут еще одно яблоко. В каждой задаче спрашивается: «Сколько стало всего?» Анализируя условие и вопрос этих задач, учащиеся выполняют математизацию реальны ситуаций: «прилететь», «прибежать», «приплыть», «положить еще» означает, что стало больше, т. е. прибавили.
Широкое включение содержательных задач в программу по математике преследует также цель обогащения словарного запаса учащихся, пополнение их представлений об окружающем мире. Так, понятие «иметь меньшую длину» с помощью задач переводится на обыденный язык по-разному: «уже», «короче», «ниже», «тоньше», «мельче».
Важную роль играют задачи и в развитии логического мышления учащихся. Целенаправленное обучение аналитико-синтетическому методу решения задач ведет к формированию у них логических операций анализа и синтеза. Школьники учатся рассуждать, доказывать, делать выводы.
б. ДИДАКТИЧЕСКИЕ ПРИНЦИПЫ НАЧАЛЬНОГО ОБУЧЕНИЯ МАТЕМАТИКЕ
Общие положения. дидактические принципы — исходные положения теории обучения, выражающие основные закономерности процесса обучения. Они определяются целями обучения и воспитания, потребностями общественного развития, особенностями учебной деятельности учащихся различных возрастов.
дидактические принципы (принципы обучения) взаимно связаны и образуют систему. В педагогической литературе встречаются различные варианты системы дидактических принципов, различающейся укрупнением или объединением отдельных принципов или, наоборот, их детализацией, разделением одного принципа на несколько.
Рассмотрим систему, в основе которой — семь принципов: воспитывающее обучение, научность, сознательность усвоения, активность учащихся, наглядность обучения, прочность знаний, индивидуальный подход. Эти принципы детально изучаются в курсе педагогики, поэтому ограничимся лишь кратким рассмотрением сущности каждого из принципов, обращая главное внимание на особенности реализации их в начальном обучении математике.
Принцип воспитывающего обучения. Всякое обучение должно быть воспитывающим, т. е. наряду с определенными обучающими функциями должны осуществляться и воспитательные функции. Отсюда, однако, не следует, что все воспитание сводится к обучению. Наоборот, по-видимому, правильнее будет считать, что обучение является составной частью системы воспитания.
Воспитание в процессе обучения вообще, и математике в частности, имеет своей основной целью формирование у школьника коммунистического мировоззрения и морали. Как решается эта задача при начальном обучении математике? На этом этапе обучения необходимо прежде всего показать, что всем изучаемым понятиям и фактам соответствуют реальные объекты, свойства и отношения между ними. Именно в начальном обучении иллюстрируется на многочисленных примерах известное утверждение Ф. Энгельса о том, что натуральные числа и геометрические фигуры взяты из реального мира, а не возникли из чистого мышления. Мы неоднократно обращаемся к реальным прообразам количественных отношений и пространственных форм, т. е. начинаем по существу формирование правильных представлений о предмете математики, о том, что математика, как и другие науки, изучает окружающий нас реальный мир.
Мораль это совокупность норм и правил поведения людей во всех сферах общественной жизни. В математике существует много правил, которые нужно строго выполнять. Воспитание строгости соблюдения разного рода математических правил (алгоритмов) способствует и воспитанию правил поведения в обществе, соблюдению норм, регулирующих отношения между людьми.
На уроках математики учитель имеет большие возможности для воспитания у учащихся честности, трудолюбия, стремления к преодолению трудностей и т. д. Важнейшим средством воспитания этих качеств являются арифметические задачи, текст которых выполняет воспитательную функцию. Воспитывающий характер обучения в значительной мере зависит также от методов преподавания.
Научность в обучении. В соответствии с этим принципом учебный материал должен излагаться в последовательности, сохраняющей связи между понятиями, темами, разделами в рамках отдельного предмета, а также межпредметные связи. Таким образом, принцип научности в обучении включает систематичность и последовательность (иногда в педагогической литературе этот принцип называют принципом научности, систематичности и последовательности в обучении).
Научность в обучении математике не означает, что в учебную программу включается система математических знаний в том виде, в котором она существует в науке математике. Применительно к начальному обучению математике принцип научности следует понимать как отражение в нем определенных математических идей, позволяющее осуществить их раннюю пропедевтику. Такими фундаментальными математическими идеями являются идеи числа, функциона4ьной зависимости, геометрической фигуры, измерения величин, алгоритма.
В начальных классах формируется представление о натуральном ряде как об упорядоченном; дискретном множестве с первым и (з
последнего элемента. Такие используемые в практике обучения выражения, как «соседние числа», «сосед справа», «сосед слева», соответствуют отношениям, рассматриваемым в науке математике, «непосредственно следует за», «непосредственно предшествует». Свойства натурального ряда «для каждого числа имеется единственный сосед справа», «для каждого числа, кроме 1, имеется единственный сосед слева», «сосед справа получается прибавлением 1», «сосед слева получается вычитанием 1» отражают идеи порядковой теории натурального ряда и значения функции прибавления единицы для формирования этого ряда.
В первом классе смысл операции сложения раскрывается через объединение множеств конкретных предметов. При этом неявно используется известное положение количественной теории и натуральных чисел: если АПВ= ®, то т(А[IВ)=т(А)+т(В).
«Открываемая» младшими школьниками зависимость между результатами и компонентами арифметических операций служит пропедевтикой идеи функциональной зависимости.
В начальных классах важно сформировать’ представление о замкнутости множества натуральных чисел относительно отдельных операций: для любых двух натуральных чисел можно найти их сумму, их произведение, но не для любых двух натуральных чисел можно найти натуральное число, равное их разности или их частному.
Ознакомление учащихся с процедурой измерения отрезков служит подготовкой к усвоению ими в дальнейшем более общих вопросов теории измерения величин.
Сознательность усвоения. Сознательность усвоения понимается как такое овладение учащимися знаниями, которое включает глубокое понимание усвоенного и умение применять его в новых конкретных ситуациях.
Трудности, связанные с реализацией принципа сознательности, обусловлены отчастI1 тем, что механизм понимания недостаточно изучен. Однако можно все же утверждать, что если ученик понял какой-то материал, то он должен уметь отвечать на такие-то вопросы, решать такие-то задачи (важно правильно подобрать соответствующие вопросы и задачи). Если же ученик не справляется с этими вопросами и задачами, значит, он не понял данный материал.
В процессе обучения учитель должен постоянно получать информацию о качестве усвоения учащимися изучаемого материала. Это особенно важно при начальном обучении математике, так как непонимание одного вопроса обусловливает непонимание последующего
материала. Чтобы выяснить, заучен материал или же понят, нужна педагогически целесообразная система вопросов и задач. Считают,
что вопрос «педагогически целесообразно» поставлен, если он вызывает активную мыслительную деятельность учащегося и не допускает ответа заученными словами из учебника.
Сознательное усвоение знаний исключает догматическое преподавание, результатом которого являются «формальные знания». Формализм чаще всего встречается при обучении математике. Это объясняется спецификой математики, в частности широким использованием в ней искусственного символического языка. Учащийся иногда ориентируется на запоминание внешнего символического выражения содержательного математического факта. Формальные знания бесполезны, так как их невозможно применять на практике. Так, ученик может знать таблицы сложения и умножения чисел, но не понимать, в каких задачах применяются действия сложения и умножения. Это является следствием отрыва символической записи сложения и умножения чисел от конкретных, реальных интерпретаций этих записей в процессе их изучения.
Активность учащихся. Сознательность усвоения предполагает активность учащихся в процессе обучения. Без активной мысли- тельной деятельности не может быть достигнуто сознательного усвоения знаний. Различают активность в широком и узком смысле. Активность в широком смысле при обучении математике существенно не отличается от активности учащихся в процессе обучения их другим предметам, т. е. она не затрагивает специфику учебного предмета. Активность же в узком смысле можно понимать как проявление специфической мыслительной деятельности, характерной для ученого-математика и называемой потому «математической» деятельностью.
На первый взгляд сама постановка проблемы обучения математической деятельности может показаться неправомерной. Действительно, способен ли ученик младших классов школы к математической деятельности? Очевидно, что к математической деятельности на высоком логическом уровне не способен ни ученик III, ни ученик Х класса. Но к какой-то математической деятельности, адекватной уровню мышления, способен и первоклассник. Все зависит от того, что мы понимаем под «математической деятельностью».
Когда первоклассник (или дошкольник) образует пары элементов из двух множеств и приходит к выводу, что в одном множестве больше предметов, чем в другом, он уже осуществляет некоторую, хотя и весьма примитивную, математическую деятельность. Усваивая понятие арифметической операции, ученик переходит от действий над множествами конкретных предметов к операциям над соответствующими числами (числами элементов этих множеств), отвлекаясь при этом от природы предметов. Это тоже математическая деятельность, но на более высоком уровне. Открывая законы действий над числами, отвлекаясь при этом от конкретных чисел, заменяя их буквами (или пустыми окошками различной формы), он осуществляет математическую деятельность на еще более высоком уровне.
Обучение математике может и должно строиться так, чтобы начиная с первого класса ученик последовательно переходил от одного уровня математической деятельности к другому, более высокому.
Известный математик-педагог д. Пойа так формулирует принцип активного учения: лучший способ изучить что-нибудь — это открыть самому. Хотя ученик третьего класса «открывает» то, что уже давно открыто, он мыслит при этом как первооткрыватель. Важная задача методики преподавания стимулировать открытия учащихся.
Наглядность обучения. Наглядное обучение, по словам К. д. Ушинского,— такое обучение, которое строится не на отвлеченных представлениях и словах, а на конкретных образах, непосредственно воспринятых ребенком. Наглядность очень важна при начальном обучении математике в связи с особенностью конкретно-образного мышления младших школьников.! В средних и старших классах широко используется символическая наглядность (чертежи, графики, графы, схемы, таблицы и др.). При начальном же обучении математике применяются все виды наглядности: натуральная, символическая и особенно изобразительная. Например, приступая к изучению числа и цифры 5, показывают различные картинки, на каждой из которых изображено множество каких-либо предметов, причем общим для всех этих множеств является лишь то, что каждое состоит из пяти элементов (карандашей, птиц, рыб, мальчиков, автомашин и т. п.)., Широкое использование изобразительной наглядности связано с тем, что на начальном этапе обучения математике математические понятия абстрагируются от их реальных прообразов. Используется также символическая наглядность, сначала в сочетании с изобразительной. Так, например, желая показать, что девочек на одной картинке столько же, сколько мячиков, изображенных на другой картинке, проводят стрелки от каждой девочки к одному из мячиков
так, чтобы никакие две стрелки не оканчивались у одного мячика. Конечно, эти стрелки можно истолковать, как обозначения выбора мячика девочкой. При формировании представлений об отношениях «меньше» и больше» рассматриваются случаи, когда всем девочкам не хватает мячиков («Леночка плачет, ей не достался мячик») и когда остаются лишние мячики. От этой изобразительно-символической наглядности до чисто симнолической наглядности
один шаг. Можно и девочек и мячик обозначать какими-нибудь фигурами, например треугольниками, кружочками или просто точками.
Любое средство символической наглядности представляет собой условную знаковую систему, с помощью которой изучаемые свойства предметов, явлений, процессов отделяются от прочих свойств. Таким образом, символическая наглядность является по существу своебразным языком. Так, например, чтобы стрелки, о которых шла речь выше, стали понятными, необходимо разъяснить, что они обозначают. То же можно сказать и о записях 5 + 3 = 8, 5.3 = 15 и т. п. Каждая из них становится наглядной лишь после того, как ее проиллюстрируют с помощью какой-нибудь реальной ситуации, которую она описывает, т. е. после того, как разъяснена ее семантика (выраженный этой записью смысл).
Часто символическая запись, например 5. 3= 15, может иллюстрироваться с помощью геометрической модели, например прямоугольника, изображенного на бумаге, длина которого 5, а ширина З клеточки. В таком случае легко определить произведение — число клеточек, содержащихся в изображенном прямоугольнике, легко «доказать» свойство коммутативности (переместительности) умножения, сосчитав число клеточек по рядам и столбцам (слово «доказать» взято в кавычки, так как это предматематическое доказательство на частном случае, модели).
Важную роль играет наглядность при формировании математических понятий. Обычно различают две ступени этого процесса:
чувственную, состоящую в формировании ощущений, восприятия и представления, и логическую, заключающуюся в переходе от представления к понятию с помощью обобщения и абстрагирования.
Прочность знаний. Сохранение у учащихся в течение длительного времени систематизированных знаний, умений и навыков возможно лишь при осознанном усвоении знаний. Сознательность усвоения обеспечивается активной мыслительной деятельностью, поэтому необходимым условием прочности знаний является приобретение их активным способом. Однако наряду с сознательностью и активностью необходима также соответствующая организация обучения, учитывающая особенности механизма запоминания. Существуют следующие общедидактические положения: а) запоминание находится в прямой зависимости от повторения; б) память имеет избирательный характер запоминается преимущественно то, что для нас существенно, интересно; в) материал запоминается лучше, когда раскрываются возможности применения его на практике; г) запоминанию способствует разделение изучаемого материала на небольшие порции по смысловому содержанию с выделением опорных пунктов в форме заголовков, вопросов, математических соотношений; д) эмоционально окрашенный материал запоминается лучше.
Вопрос о том, что должен запомнить ученик из изучаемого материала, гораздо сложнее, чем может показаться на первый взгляд. Совершенно очевидно, что запомнить все невозможно да и не нужно, если имеется в виду весь школьный курс математики. В курсе же математики начальных классов почти все подлежит запоминанию:
таблицы сложения и умножения однозначных чисел, алгоритмы выполнения четырех арифметических действий над многозначными числами и т. д.
Повторение ранее изученного материала перед изучением новой темы является одним из важнейших видов повторения при обучении математике вообще и в начальных классах в частности. Оно способствует лучшему запоминанию как старого, так и нового материала.
Индивидуальный подход в обучении. При обучении необходимо учитывать особенности мышления каждого ученика, свойства его памяти, отдельных анализаторов (зрение, слух) и т. д. даже у учащихся одного возраста они различны, поэтому один и тот же материал одни учащиеся усваивают быстрее, а другие медленнее. Все это и обусловливает необходимость индивидуального подхода в обучении.
Если бы можно было как-то «измерить» скорость усвоения математического материала различными учащимися, то разброс был бы намного больше, чем по другим предметам. Ориентирование на «среднего» ученика приводит к отрицательным последствиям. Слабые учащиеся, находящиеся ниже уровня «среднего», становятся неуспевающими, а сильные начинают скучать на уроках и теряют интерес
к предмету. Поэтому в условиях классно-урочной системы, когда в классе одновременно обучается ЗО—40 человек, необходимо осуществлять принцип индивидуального подхода, использовать различные приемы, учитывающие особенности усвоения материала различными учащимися (дифференцированные задания, опережающие, выравнивающие занятия, дополнительные индивидуальные занятия, кружковые занятия и т. п.).
Одно из возможных решений проблемы индивидуального подхода связано с использованием в обучении персональных компьютеров.
7. МЕТОДЫ ОБУЧЕНИЯ МАТЕМАТИКЕ
Общие и специальные методы. В дидактической литературе встречаются различные определения понятия «метод обучения»... Будем исходить из достаточно широко распространенного представления о методах обучения как об упорядоченных способах взаимосвязанной деятельности учителя и учащихся, направленных на достижение целей обучения как средства образования и воспитания. Описание каждого метода обучения должно раскрывать: 1) обучающую деятельность учителя; 2) содержание учебной (познавательной) деятельности ученика; З) связь между ними, т. е. способ, с помощью которого учитель управляет познавательной деятельностью учащихся.
В дидактике рассматриваются, однако, лишь общие методы обучения, т. е. методы, не учитывающие специфики отдельных предметов. Исследование возможностей конкретной реализации общих методов в начальном обучении математике путем их модификации, адаптации с учетом специфики математики и мыслительной деятельности учащихся начальных классов является предметом методики начального обучения математике. Используются также специальные методы обучения, отражающие особенности математического познания.
Специальные методы обучения, и прежде всего метод моделирования (построения математических моделей), в наибольшей степени влияют на формирование и развитие математического стиля мышления.
Репродуктивные и продуктивные методы. Методы обучения разделяют на две группы: одни из них ориентированы в основном на передачу учащимся готовых знаний, другие стимулируют познавательную деятельность по приобретению новых знаний. Используя методы первой группы, учитель излагает, объясняет учебный материал, привлекает различные средства наглядности и другие дидактические средства, а ученики воспринимают информацию, усваивают ее, а затем воспроизводят по требованию учителя. Такие методы называют репродуктивными. Развивающий эффект их использования в обучении недостаточно высок, так как они не вызывают активной мыслительной деятельности учащихся. Приведение методов обучения в соответствие с требованиями реформы школы означает целесообразное сочетание оправдавших себя на практике репродуктивных методов с методами, ориентированными на обучение деятельности по самостоятельному приобретению новых знаний, называемыми также продуктивными.
Продуктивные методы не противопоставляются репродуктивным. Речь идет о дидактически целесообразном сочетании этих методов на различных этапах обучения в зависимости от целей и содержания обучения.
В начальном обучении математике ведущую роль играют репродуктивные методы, так как у учащихся формируется база знаний и умений, на основе которой уже можно строить обучение простейшей познавательной деятельности.
Общеизвестна роль задач в обучении математике и развитии математического мышления учащихся. Уровень усвоения математических знаний и математического мышления учащихся проверяется с помощью задач. Поэтому методы обучения решению задач следует отнести к специфическим методам обучения математике.
Эмпирические методы. Наблюдение, опыт, измерения — эмпирические методы, используемые при изучении экспериментальных естественных наук,— не являются специфичными для математики. Однако в начальном обучении математике эти методы должны широко применяться в качестве эвристических. Например, изучение понятия «квадрат» учащиеся начинают с рассмотрения множества предметов, отличающихся друг от друга формой, размерами, окраской, материалом, из которого они сделаны. дети, после того как им показывают одну из этих фигур и говорят, что это квадрат, безошибочно отбирают из множества предметов те, которые имеют такую же форму, пренебрегая различиями, касающимися размеров, окраски, материала. Здесь выделение из множества предметов подмножества производится по одному, возможно, еще неосознанному признаку — по форме. Школьники еще не знают свойств квадрата, они распознают его только по форме. Такое распознавание встречается уже у дошкольников. дальнейшая работа по формированию понятия «квадрат>) состоит в анализе этой формы с целью выявления ее свойств.
Опытным же путем учащиеся «открывают» практически все свойства арифметических операций (переместительности и сочетательности сложения, свойство распределительности умножения относительно сложения), функциональных зависимостей (прямой и обратной пропорциональности), геометрических фигур.
Опыт в математике, конечно, не доказательство, однако может использоваться при начальном обучении как эвристический прием.
Сравнение и аналогия. Сравнение и аналогия — логические методы, используемые как в научных исследованиях, так и в обучении. В результате сравнения выявляются сходство и различие сравниваемых предметов, т. е. наличие у них общих и необщих (различных) свойств. Например, сравнивая квадрат и прямоугольник, мы обнаруживаем общие свойства: четыре стороны, четыре вершины, четыре угла, все углы прямые, а также различия: в квадрате все стороны равны, в прямоугольнике — только противоположные (имеется в виду разносторонний прямоугольник). При сравнении равенств 3+5=5+3 и 4+6=6+4 обнаруживается очень важное их свойство, которое служит основой для дальнейшего обобщения: в каждом равенстве знаком «=» связаны две суммы, различающиеся только порядком слагаемых.
Правильный вывод можно получить, если выполняются следующие условия: а) сравниваемые понятие однородны; б) сравнение осуществляется по существенным признакам. Оба эти условия выполняются в приведенных выше сравнениях: а) квадрат и прямоугольник — однородные понятия (четырехугольники), записи 5+3= =3+5 и 4+6=6+4 равенства арифметических выражений; б) сравнение произведено по существенным признакам, служащим основой для определения квадрата и прямоугольника в первом случае, и для обобщения и открытия закона коммутативности сложения во втором.
Сравнение подготавливает почву для применения аналогии. Сущность вывода заключения по аналогии состоит в следующем. Если у объектов а и Ь имеются общие признаки Р1,,Р2, •. Р а у объекта а обнаружено, кроме того, свойство Рп+1, утверждают, что и Ь обладает свойством Рп + 1. Правильное использование аналогии предполагает следующее: 1) число общих свойств объектов а и Ь должно быть как можно большим; 2) необходимо, чтобы общие признаки Р1 Рп были, специфичными для рассматриваемых объектов и по возможности более разнородными, максимально отличающимися друг от друга; 3) свойство Рп+ 1, о котором говорится в заключении, полученном с помощью аналогии, и свойства рi Рп должны быть однотипными; 4) переносимый признак Рп + 1 не должен иметь специфического характера. Например, сложение обладает свойствами переместительности и сочетательности, умножение свойством переместительности. Это наводит на мысль, что и умножение обладает свойство сочетательности.
Как видно, рассуждение по аналогии имеет лишь правдоподобное, вероятное, но не достоверное заключение, поэтому аналогия служит эвристическим приемом для формулировки гипотез, открытия новых свойств изучаемых объектов. Она может привести и к неверным предположениям, поэтому заключение по аналогии подлежит проверке. В начальном обучении математике имеются возможности для применения аналогии. Выявление сходства и различия между реальными ситуациями позволяет описать их с помощью одних и тех же или различных математических соотношений. Например, на одной картинке изображено 5 красных цветков и 4 синих. По этой картинке можно составить такие задачи: «На сколько больше красных цветков, чем синих?», «На сколько меньше синих цветков, чем красных?», «Сколько всего цветков?» и др.
На другой картинке изображено 7 больших птичек и З маленькие. Сходство условий подсказывает нам возможность распространения этого сходства и на задачи, т. е. по аналогии учащиеся составляют задачи и ко второй картинке. Иногда говорят, что это — деятельность по образцу. В действительности же здесь имеет место рассуждение по аналогии. Не нужно опасаться ложных аналогий. Анализ ошибочных заключений представляет собой полезный прием обучения. Так, ученик, зная, что
написал по аналогии:
3 (4+5)=3• 4+3 5,
3 (4+5)= (3+4) (3+5), (2)
т. е. свойство распределительности умножения относительно сложения распространил на сложение относительно умножения. Путем вычисления устанавливается, что равенство (2) неверно. Эту ошибку и необходимо использовать для того, чтобы подчеркнуть, что свойство распределительности имеет место только для умножения относительно сложения, но не для сложения относительно умножения. Иными словами, чтобы умножить число на сумму двух чисел, можно умножить это число на каждое слагаемое и полученные произведения сложить, но чтобы сложить число с произведением двух чисел, нельзя складывать его с каждым сомножителем и полученные суммы перемножать.
Обобщение, абстрагирование, конкретизация. Логические приемы (обобщение, абстрагирование, конкретизация) находят ограниченное применение в начальном обучении математике. Это объясняется тем, что обобщение и абстрагирование используются почти всегда совместно при переходе от представлений к понятиям. В начальном же обучении во многих случаях мы остаемся на уровне представлений, т. е. не доводим процесс познания до формирования понятий.
Однако применение этих приемов, пусть ограниченное, в начальном обучении математике возможно. Например, приемы обобщения и абстрагирования могут использоваться при рассмотрении частных случаев переместительности сложения. В результате учащиеся приходят к общей закономерности «а + Ь = Ь + а для любых а, Ь». В свою очередь эта закономерность конкретизируется для частных случаев (7+3=3+7).
Понятие натурального числа формируется у учащихся в несколько приемов. Сначала учитель предоставляет детям возможность сравнивать множества различных предметов по их численности. Обнаруживается, что между элементами некоторых множеств удается установить взаимно однозначное соответствие. Выделяются классы равночисленных множеств, которым в качестве характеристик приписываются определенные натуральные числа. Здесь ученик уже имеет дело с абстракцией от абстракции: от множества предметов он переходит к классу равночисленных множеств, а затем — к свойству класса (численность принадлежащих классу равночисленных множеств).
Индукция и дедукция. Восхождение от частного к общему, от фактов, установленных с помощью наблюдения и опыта, к общим закономерностям имеет логическую форму рассуждения «от частного к общему». Вывод общего заключения из частных посылок называется индукцией. В начальной школе возможно использование индукций двух видов: полно и неполной. Индукция бывает полной, если частные посылки исчерпывают все возможные случаи, и неполной.
Говоря об использовании индукции в обучении, имеют в виду, как правило, неполную индукцию. Например, сколько бы мы ни приводили равенств, отражающих переместительность сложения или умножения, невозможно исчерпать все частные случаи, так как пар натуральных чисел бесконечно много. Неполная индукция не может, разумеется,. служить методом доказательства в математике. Но она является мощным эвристическим методом.
Сколько же надо рассмотреть частных посылок, чтобы подвести учащихся к открытию общей закономерности, общего правила, алгоритма? На этот вопрос, очевидно, нельзя дать исчерпывающего ответа. Необходимо, чтобы частное содержание, которое выражается в посылках и не входит в общее заключение, варьировалось, т. е. видоизменялось от посылки к посылке. Это помогает школьникам выявить то общее, неизменное, что должно составлять содержание заключения. Использование индукции иногда бывает малоэффективным, например когда учащимся предлагаются однотипные, малоразличимые посылки. Так, известный алгоритм умножения многозначного числа на однозначное, как и другие алгоритмы, изучаемые в начальных классах, мы не можем описать в общем виде. В процессе его изучения рассматривается следующая система частных случаев:
все цифры многозначного множителя значимые, многозначный множитель оканчивается нулем (нулями), этот множитель содержит нуль (нули) в середине. Если эта система рассматривается не в полном объеме, учащиеся могут столкнуться с серьезными трудностями.
При формировании простейших геометрических понятий наряду с наблюдением, опытом, измерениями используется и индукция. Чтобы абстрагировать общую форму, необходимо рассматривать не один, а много квадратов, различающихся размерами, окраской, материалом, из которого они изготовлены. В каждом из квадратов школьники обнаруживают четыре- равные стороны, четыре прямых угла, затем по индукции приходят к заключению, что во всяком квадрате четыре стороны и четыре прямых угла.
Дедуктивное рассуждение, которое определяют как рассуждение от общего к частному, отличается от индуктивного (в смысле неполной индукции) достоверностью заключения, которое истинно по крайней мере тогда, когда истинны все посылки. В дедуктивном рассуждении нельзя получить ложное заключение из истинных посылок. Именно поэтому дедуктивные рассуждения используются в математических доказательствах.
дедукция как метод обучения математике включает обучение дедуктивным доказательствам и преобразованию совокупности предложений, полученных опытным путем либо с помощью аналогии, индукции или других эвристических методов, в систему предложений, упорядоченных отношением следования, которая расширяет уже известный фрагмент теории. Какова же роль дедукции в начальном обучении математике? Имеет ли какое-то отношение пресловутая математическая строгость к начальному обучению? Какие учебные или воспитательные цели оправдывают или, наоборот, отвергают ориентацию на какой-то уровень строгости в начальном обучении? Целесообразность раннего обучения детей точным рассуждениям и убедительным обоснованиям не вызывает сомнений. Однако возможно ли обучение доказательству младших школьников? Не предполагают ли математические доказательства недоступного для учащихся 1—1У классов уровня абстракции? Ответы на поставленные вопросы зависят от того, что понимают под доказательством на начальном этапе обучения математике, или под предматематическим доказательством
8. ОБУЧЕНИЕ МЛАДШИХ ШКОЛЬНИКОВ ПРЕДМАТЕМАТИЧЕСКОМУ
ДОКАЗАТЕЛЬСТВУ
Одной из наиболее сложных задач обучения математике является формирование у учащихся средней школы умения доказывать математические предложения. Успешность ее решения во многом зависит от того, насколько целенаправленно и качественно ведется соответствующая подготовительная работа в начальных классах. По мнению психологов М. М. Вахрушева, Л. Ф. Войтко, А. В. Запорожца,
М. В. Крыловой, К. А. Некрасоой,В. А. Филя, такая работа может начинаться уже с 1 класса. Подготовка младших школьников к сознательному усвоению и проведению строгих математических доказательств предполагает: 1) воспитание у детей потребности в аргументации высказываемых суждений и осознание ими необходимости доказательств; 2) использование в обучении доступных для данного возраста способов обоснования истинности математических предложений и постепенное овладение учениками наиболее употребительными из них. Такая подготовительная работа может успешно (и без дополнительной нагрузки учащихся) проводиться в рамках современного начального курса математики, так как в его содержании заложены объективные предпосылки для повышения логической грамотности детей. Об этом свидетельствуют анализ учебников математики для начальной школы, методических рекомендаций к ним, изучение передового педагогического опыта.
Воспитание потребности и навыков аргументации суждений начинается с постоянно задаваемого учителем вопроса «Почему?», выполнения заданий с требованиями «Объясни», «Докажи».
Возрастные особенности мышления младших школьников и отсутствие у них логически стройной системы знаний обусловливают невозможность или, по крайней Мере, ограниченность использования дедуктивных доказательств. Например, целью одного из первых уроков, на котором изучается нумерация чисел первого десятка, является установление порядковых отношений между числами изученного отрезка натурального ряда 1, 2: вывод, чтение и запись математических предложений: 1=1, 1.с2, 21, 2=2. Каждое из них должно быть доказано. Как же это сделать? Из психологии нам известно, что для детей 6—7 лет необходимо обеспечить наглядную основу формируемого знания, поэтому обратимся к средствам наглядности (реальным объектам из окружающей действительности, картинкам с изображением знакомых детям предметов; счетным палочкам; геометрическим фигурам и т. п.). Рассмотрим один из возможных вариантов организации учебной деятельности первоклассников на этом уроке.
— Положите один круг, а под ним столько же треугольников. Сколько треугольников надо положить? (Тоже один.)
Почему? (Потому что треугольников должно быть столько же, сколько кругов, а круг у нас один.)
— Обозначьте цифрой число кругов и число треугольников. (Ученики выставляют карточки с цифрой 1.)
— Мы говорили, что кругов и треугольников у нас поровну. На математическом языке слово «поровну заменяют знаком <=. (далее учитель вводит термин «равно и привлекает учащихся к анализу символа для обозначения этого отношения.)
— Как же на математическом языке записать, что кругов и треугольников у нас поровну, по одному? (1 = 1.)
— Прочитайте хором эту запись. А теперь положите рядом с треугольником еще один треугольник. Сколько их стало? (2.)
— Обозначьте число треугольников цифрой. (Ученики заменяют в ряду треугольников карточку с цифрой i на карточку с цифрой 2.)
— Можно сказать, что и сейчас у нас кругов и треугольников поровну? (Нет, теперь у нас кругов меньше на 1, а треугольников больше на 1.)
— А почему треугольников стало больше, чем кругов? (Потому что их было столько же, сколько кругов, да мы положили еще один.) ‘
— Треугольников у нас два (учитель на наборном полотне выставляет карточку с цифрой 2), а кругов один (выставляет карточку с цифрой i). Треугольников больше, чем кругов, значит два больше, чем один. Скажем это хором: «два больше, чем один.
— На математическом языке это предложение записывают так: 2. i. Прочитайте, что у нас написано.
— давайте сравним значки для обозначения слов «равно и «больше. Чем они похожи? А чем различаются? (После такого анализа и сравнения символов учитель подчеркивает, что острие значка «всегда показывает на меньшее число.)
— Итак, треугольников у нас больше. Это мы записали: 2. i. А что можно сказать о числе кругов? (Кругов меньше, чем треугольников. Один меньше, чем два.)
— Кто догадался, как на математическом языке можно записать предложение «Один меньше, чем два? (дети складывают из цифр и знаков выражение i 2. Затем вызванный к доске ученик выполняет ее на общеклассном наборном полотне, класс хором читает это выражение.)
Положите в верхний ряд еще один круг. Сколько стало кругов? Обозначьте их число цифрой. (2.)
— Что можно сейчас сказать о числе кругов и треугольников? (Их опять поровну. треугольников и кругов по два.)
— Кто сумеет на математическом языке записать, что кругов и треугольников у нас поровну, по два? (дети самостоятельно составляют равенство 2= 2 и читают его.)
далее учитель переходит к обобщению и закреплению приобретенных знаний. На наборном полотне составляются четыре записи:
1 = 1, 2. 1, 1.2, 2=2. Учащимся предлагается прочитать их и доказать с помощью палочек красного и белого цвета. докажем, например, что 1 «2. (Возьмем 1 белую палочку и 2 красные. Белых палочек меньше, чем красных, потому что если соединять в пары палочки разного цвета, одной белой палочки не хватает.) Аналогично обосновывается истинность каждого из остальных предложений.
На последующих уроках изучения нумерации чисел в пределах десяти дети подводятся путем индуктивного обобщения к выводу принципа построения натурального ряда чисел: каждое число ряда больше всех чисел, встречающихся при счете раньше этого числа, и меньше любого числа, которое при счете называется после него. Этот вывод выступает уже в качестве нового аргумента доказательства утверждений вида 6.с7 (так как при счете «шесть называют раньше «семи»).
Рассмотренный пример позволяет сделать некоторые выводы:
1) опыт, практическая деятельность детей являются не только источником математических понятий и суждений о них, но и служат средством проверки соответствия этих суждений действительности; 2) аргументы доказательства могут изменяться по мере накопления младшими школьниками обобщенных знаний о математических объектах; 3) используемые в начальном обучении математике способы обоснования истинности предложений отличаются от строгих математических доказательств прежде всего тем, что опираются на эксперимент, проводимый на модели конкретной ситуации. В то же время эти способы имеют сходство с общепринятыми в математике доказательствами: а) у них общая цель обосновать истинность утверждения о математических объектах; б) и те и другие строятся посредством выведения
 2015-07-14
2015-07-14 6990
6990
