Зададимся вопросом: какова вероятность 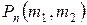 того, что в условиях схемы Бернулли событие А, имеющее вероятность
того, что в условиях схемы Бернулли событие А, имеющее вероятность 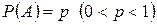 , при
, при 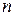 испытаниях появляется не менее
испытаниях появляется не менее 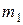 раз и не более
раз и не более 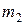 раза?
раза?
Введем функцию Лапласа:
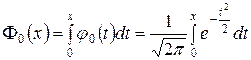 , (11)
, (11)
Интеграл 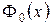 не выражается через элементарные функции, для его вычисления используются специальные таблицы. Функция
не выражается через элементарные функции, для его вычисления используются специальные таблицы. Функция 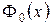 обладает следующими свойствами:
обладает следующими свойствами:
1) 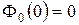 ;
;
2) 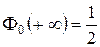 ;
;
3) 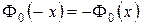 , то есть функция нечетна;
, то есть функция нечетна;
4) 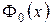 - монотонно возрастающая функция;
- монотонно возрастающая функция;
5) при 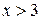 , с точностью до тысячных, можно принять
, с точностью до тысячных, можно принять 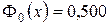 .
.
Интегральная теорема Муавра – Лапласа. Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы 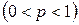 , то при
, то при 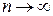 вероятность появления события А ровно в n независимых испытаниях не менее
вероятность появления события А ровно в n независимых испытаниях не менее 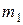 раз и не более
раз и не более 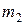 раз приближенно равна
раз приближенно равна
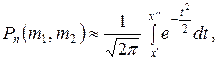 (12)
(12)
где 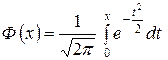 - функция Лапласа, значения которой определяются таблично,
- функция Лапласа, значения которой определяются таблично, 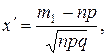
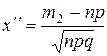 .
.
Замечание 1. Для того, чтобы можно было пользоваться таблицей функции Лапласа, соотношение (12) преобразуют к виду:
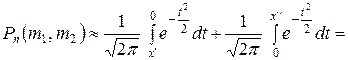
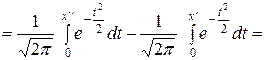
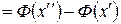 .
.
Замечание 2. Функция Лапласа является нечетной функцией 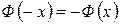 . При
. При 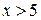 можно принять
можно принять 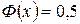 .
.
Пример. Вероятность того, что деталь не прошла проверку ОТК, равна 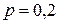 . Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение. По условию 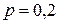 ,
, 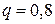 ,
, 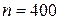 ,
, 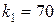 ,
, 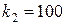 . Воспользуемся интегральной теоремой Лапласа:
. Воспользуемся интегральной теоремой Лапласа:
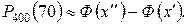
Найдем

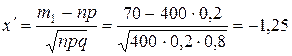 ,
,

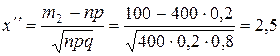 .
.
Таким образом, получим:

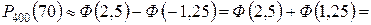

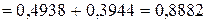 .
.
 2015-07-03
2015-07-03 1161
1161
