Передаточные функции используют преобразования Лапласа.
Преобразование Лапласа его свойства.
Оригинал изображения по Лапласу
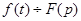
р – комплексная величина, оператор Лапласа.
Формула преобразования Лапласа: 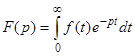
Преобразование Лапласа заменяет решение дифференциальных уравнений во временной области, решением алгебраических уравнений в плоскости р,что облегчает задачу.
Свойства преобразования Лапласа
1. Линейность
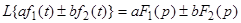
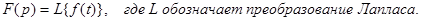
Таким образом преобразование Лапласа от суммы равно сумме преобразований Лапласа.
2. Изображение производных.
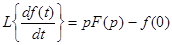
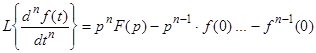
3. Преобразование Лапласа от интеграла (Изображение интеграла).
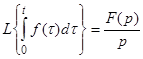
4. Изображение Лапласа от функции с запаздывающим аргументом.
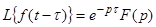
Функция с запаздывающим аргументом:
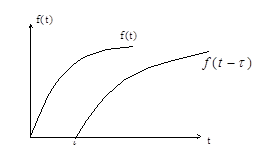 |
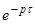 - оператор запаздывания.
- оператор запаздывания.
5. Теорема о конечном значении.
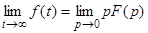
Если предел существует, это означает, что поведение функции в бесконечности, определяется поведением её изображения в нуле.
Понятие передаточной функции.
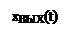

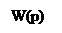



Передаточной функцией (W(p)) называется отношение изображения выходного сигнала при нулевых начальных условиях (ННУ).
ННУ – означают, что входной и выходной сигнал вместе с их (n-1) производными равен нулю.
1. Пример получения передаточной функции.
Передаточная функция ГПТ.
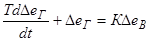
Воздействуем оператором Лапласа на правую и левую дифференциального уравнения.

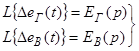 Введем обозначения.
Введем обозначения.
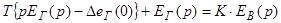
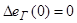
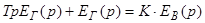
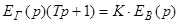
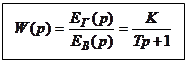
 2014-02-02
2014-02-02 2969
2969
