Нелинейная катушка представляет собой катушку, намотанную на замкнутый ферромагнитный сердечник, для которого зависимость магнитного потока в магнитопроводе от протекающего по обмотке тока нелинейная. Индуктивное сопротивление таких катушек, оказываемое переменному току, не постоянно, так как
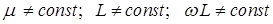 .
.
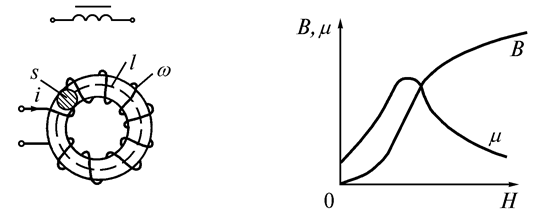 |
На рис. 6.7 а показана катушка с ферромагнитным магнитопроводом (число витков катушки
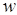 , сечение магнитопровода
, сечение магнитопровода 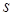 и средняя длина магнитной линии
и средняя длина магнитной линии 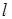 ). Такая катушка является нелинейным элементом за счет нелинейная зависимость
). Такая катушка является нелинейным элементом за счет нелинейная зависимость 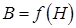 материала сердечника (рис. 6.7 б).
материала сердечника (рис. 6.7 б). а) б)
Рис. 6.7
Прохождение переменного тока через катушку с ферромагнитным магнитопроводом сопровождается магнитным гистерезисом и возникновением вихревых токов. Эти явления вызывают дополнительные потери в катушке. Потери мощности на гистерезис 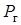 пропорциональны частоте тока
пропорциональны частоте тока 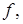 площади петли гистерезиса (рис. 7.1) и объему магнитопровода. Определяются они по различным эмпирическим формулам, например,
площади петли гистерезиса (рис. 7.1) и объему магнитопровода. Определяются они по различным эмпирическим формулам, например,
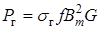 при
при 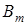 = 1,0...1,6 Тл,
= 1,0...1,6 Тл,
где 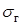 – коэффициент, зависящий от сорта стали;
– коэффициент, зависящий от сорта стали; 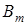 – амплитуда магнитной индукции;
– амплитуда магнитной индукции; 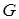 – масса магнитопровода.
– масса магнитопровода.
Потери мощности от вихревых токов рассчитывают по эмпирической формуле
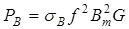 ,
,
где 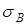 – коэффициент, зависящий от сорта стали и размеров стальных листов.
– коэффициент, зависящий от сорта стали и размеров стальных листов.
Для уменьшения потерь от вихревых токов магнитопровод выполняют не сплошным, а в виде пакета из стальных листов, изолированных друг от друга. Так, например, при частоте = 50 Гц применяют листы толщиной 0,25¼0,5 мм а при частотах порядка сотен и тысяч герц – 0,02¼0,05 мм.
Потери в магнитопроводе от гистерезиса и вихревых токов называют потерями в стали 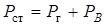 .
.
Таким образом, цепи переменного тока с ферромагнитными магнитопроводами являются нелинейными цепями, так как наличие магнитопровода приводит к искажению кривой тока.
6.3.2. Схема замещения и векторная диаграмма катушки
с ферромагнитным магнитопроводом
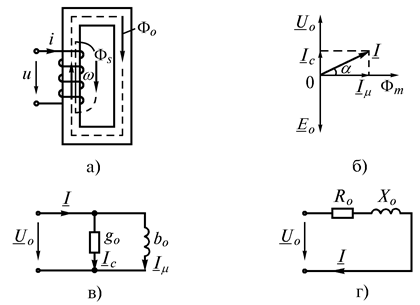 |
Рассмотрим процессы в катушке с замкнутым ферромагнитным магнитопроводом, обмотка которой имеет
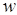 витков. Протекающий по обмотке ток
витков. Протекающий по обмотке ток 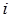 (рис. 6.8 а) создает магнитный поток. Основная часть этого потока
(рис. 6.8 а) создает магнитный поток. Основная часть этого потока 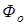 – замыкается по магнитопроводу, а меньшая часть – поток рассеяния
– замыкается по магнитопроводу, а меньшая часть – поток рассеяния 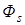 , рассеивается в пространство. Обычно
, рассеивается в пространство. Обычно 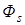 составляет несколько процентов от
составляет несколько процентов от 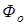 . Если магнитопровод насыщен или имеет большой воздушный зазор, то поток
. Если магнитопровод насыщен или имеет большой воздушный зазор, то поток 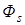 соизмерим с
соизмерим с 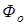 .
. Рис. 6.8
Если пренебречь активной составляющей сопротивления катушки и потоком рассеяния, то при питании катушки от источника синусоидального тока в ней будет возникать основной магнитный поток
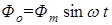 . (6.4)
. (6.4)
Вследствие этого в витках катушки возникает ЭДС самоиндукции
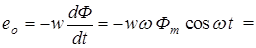
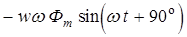 . (6.5)
. (6.5)
Так как эта ЭДС равна напряжению источника, то
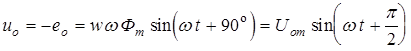 . (6.6)
. (6.6)
Формулы (6.4) и (6.6) показывают, что вектор 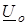 опережает вектор
опережает вектор 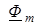 на 90°.
на 90°.
Действующее значение этого напряжения
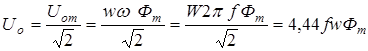 . (6.7)
. (6.7)
Построим векторную диаграмму идеальной катушки (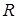 = 0,
= 0, 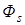 = 0). За исходный вектор примем вектор максимального значения магнитного потока
= 0). За исходный вектор примем вектор максимального значения магнитного потока 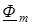 (рис. 6.8 б). Вектор напряжения
(рис. 6.8 б). Вектор напряжения 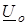 опережает вектор магнитного потока на 90°, а вектор ЭДС самоиндукции
опережает вектор магнитного потока на 90°, а вектор ЭДС самоиндукции 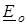 равен вектору напряжения
равен вектору напряжения 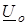 , но противоположен по направлению. Вектор действующего значения тока через катушку
, но противоположен по направлению. Вектор действующего значения тока через катушку 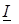 опережает вектор
опережает вектор 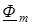 на угол
на угол 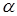 , обусловленный гистерезисом. Представим вектор
, обусловленный гистерезисом. Представим вектор 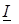 суммой двух составляющих: активной – проекцией вектора тока на вектор напряжения
суммой двух составляющих: активной – проекцией вектора тока на вектор напряжения 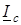 и реактивной
и реактивной 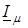 , которую принято называть током намагничивания. Тогда
, которую принято называть током намагничивания. Тогда
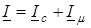 . (6.8)
. (6.8)
Этому уравнению соответствует схема замещения (рис. 6.8 в), где ток 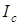 обусловлен потерями в магнитопроводе:
обусловлен потерями в магнитопроводе:
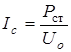 . (6.9)
. (6.9)
Составляющая 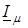 – это ток через идеализированную катушку (катушка, в магнитопроводе которой нет потерь энергии).
– это ток через идеализированную катушку (катушка, в магнитопроводе которой нет потерь энергии).
Схему на рис. 6.8 в можно преобразовать в другую схему (рис. 6.8 г), используя проводимости ветвей
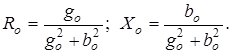
В схемах (рис. 6.8 в и г) 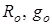 – соответственно активная составляющая сопротивления и активная составляющая проводимости, учитывающие потери мощности в магнитопроводе;
– соответственно активная составляющая сопротивления и активная составляющая проводимости, учитывающие потери мощности в магнитопроводе; 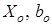 – реактивная составляющая сопротивления и реактивная составляющая проводимости, обусловленные основным магнитным потоком.
– реактивная составляющая сопротивления и реактивная составляющая проводимости, обусловленные основным магнитным потоком.
В схеме замещения реальной катушки учитываем активное сопротивление катушки 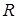 и реактивное сопротивление
и реактивное сопротивление 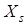 , обусловленное магнитным потоком рассеяния (рис. 6.9 а, б). В этих схемах участок ab называют ветвью намагничивания.
, обусловленное магнитным потоком рассеяния (рис. 6.9 а, б). В этих схемах участок ab называют ветвью намагничивания.
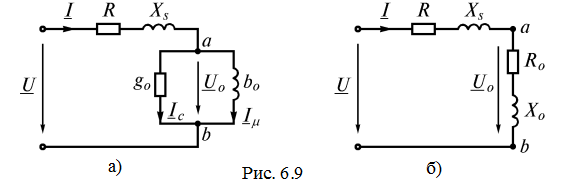
Запишем уравнение по второму закону Кирхгофа для схем (рис. 6.9) в комплексной форме
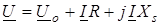 . (6.10)
. (6.10)
Применим это уравнение для построения векторной диаграммы реальной катушки (рис. 6.10). Угол, обусловленный гистерезисом
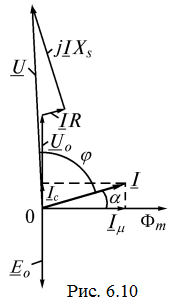
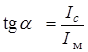 .
.
Практически 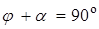 или
или 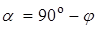 .
.
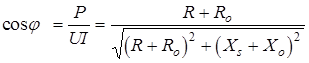 . (6.11)
. (6.11)
Активная мощность катушки с ферромагнитным магнитопроводом состоит из потерь мощности в проводах 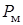 и потерь мощности в магнитопроводе
и потерь мощности в магнитопроводе 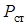
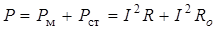 . (6.12)
. (6.12)
Чем больше угол 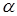 , тем больше активная составляющая тока
, тем больше активная составляющая тока 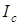 и потери в магнитопроводе. Поэтому угол
и потери в магнитопроводе. Поэтому угол 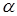 называют углом потерь в магнитопроводе.
называют углом потерь в магнитопроводе.
 2015-07-04
2015-07-04 2036
2036