Корреляционная связь

В природе многие явления и процессы взаимосвязаны между собой. В физической культуре и спорте, в спортивной команде и в организме спортсмена тоже существует много взаимосвязей между различными признаками. Например, с повышением количества занимающихся в каком-либо виде спорта повышаются результаты в этом виде; осложнения во взаимоотношениях между игроками одной команды ухудшает ее результативность; с повышением интенсивности нагрузки у спортсмена повышается пульс, увеличивается скорость кровотока в работающих мышцах, уменьшаются в них энергетические ресурсы; регулярность тренировок, оптимально подобранные нагрузки по их виду, объему и интенсивности улучшают результаты спортсмена и т.д.

Влияние одних признаков на другие может быть положительным и отрицательным. Грамотный специалист должен хорошо разбираться в таких взаимосвязях в своей области, устранять или уменьшать негативное влияние и уметь своевременно и в достаточной мере использовать полезные взаимосвязи.

Некоторые методы математической статистики могут помочь любому специалисту выявить взаимосвязи, раскрыть их особенности. Одним из таких методов и является метод корреляционного анализа. Он направлен на то, чтобы на основе статистического материала выявить факт влияния одного признака на другой, установить полезность или вред этого влияния и оценить уверенность в полученных выводах.

Будем говорить, что между двумя признаками Х и У существует корреляционная зависимость (взаимосвязь), при которой с изменением одного признака изменяется и другой, но каждому значению признака Х могут соответствовать разные, заранее непредсказуемые значения признака У, и наоборот.

Для различия направленности влияния одного признака на другой введены понятия положительной и отрицательной связи.

Если с увеличением (уменьшением) одного признака в основном увеличиваются (уменьшаются) значения другого, то такая корреляционная связь называется прямой или положительной.

Если с увеличением (уменьшением) одного признака в основном уменьшаются (увеличиваются) значения другого, то такая корреляционная связь называется обратной или отрицательной.

При постановке вопроса о корреляционной зависимости между двумя статистическими признаками Х и Y проводят эксперимент с параллельной регистрацией их значений.

Часто для определения достоверности взаимосвязи между двумя признаками (Х и Y) используют непараметрический (ранговый) коэффициент корреляции Спирмена. Вычисление данного коэффициента корреляции основано на определении разности рангов по каждой паре параметров для одного объекта. Величина этого показателя корреляционной связи определяется по формуле 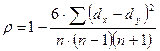(6):

(6)

где: d_x — ранги статистических данных признака х;

d_y — ранги статистических данных признака у.

n — число коррелируемых пар статистических данных признаков Х и Y

Этот коэффициент обладает такими мощными признаками:

1. На основании коэффициента корреляции можно судить только о прямолинейной корреляционной взаимосвязи между признаками.

2. Значения коэффициента корреляции есть безразмерная величина, которая не может быть меньше -1 и больше +1, т.е.

3. Если значение коэффициента корреляции равно нулю, то связь между признаками Х и Y отсутствует.

5. Если значение коэффициента корреляции отрицательное, то связь между признаками Х и Y обратная.

6. Если значение коэффициента корреляции положительное, то связь между признаками Х и Y прямая (положительная).

7. Если коэффициент корреляции принимает значения +1 или -1, то связь между признаками Х и Y линейная (функциональная).

8. Только по величине коэффициента корреляции нельзя судить о достоверности корреляционной связи между признаками. Эта достоверность еще зависит от числа степеней свободы. Она определяется по формуле (7).

ν = n – 2 (7)

Чем больше n, тем выше достоверность связи при одном и том же коэффициенте корреляции.

Если коэффициент корреляции при расчете получился отличным от нуля, то из этого еще нельзя сделать вывод о том, что коэффициент корреляции генеральной совокупности так же отличается от нуля.

Для того чтобы окончательно убедиться в наличии статистической зависимости между параметрами, проводят проверку достоверности выборочного коэффициента корреляции.

При оценке статистической достоверности коэффициентов корреляции наиболее часто встают два вопроса:

1) существенно ли отличается ли данный коэффициент от нуля (т.е. существует ли статистическая зависимость между явлениями?)?

2) в каких доверительных границах лежит истинный коэффициент корреляции в генеральной совокупности?

В практике ФКС оценка статистической достоверности различий выборок означает решение множества практических задач. Например, введение новых методик обучения, программ, комплексов упражнений, тестов, контрольных упражнений связано с их экспериментальной проверкой, которая должна показать, что испытуемая группа принципиально отличается от контрольной. Поэтому применяют специальные статистические методы, называемые критериями статистической достоверности, позволяющие обнаружить наличие или отсутствие статистически достоверного различия между выборками. Критетий Стьюдента, названный в честь английского ученого К. Госсета (Стьюдент – псевдоним), открывшего данный метод, наиболее часто применяется на практике.

Критерий Стьюдента определяется по формуле 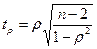(8):

(8)

далее с учетом числа степеней свободы по таблице определяют критическое значение критерия Стьюдента t_кр.

Если t_ρ>t_кр, то делают вывод о том, что выборочный коэффициент ρ значимо отличается от нуля и данные параметры действительно связаны корреляционной зависимостью.

Если t_ρ≤t_кр, отличие коэффициента ρ от нуля незначительны и корреляционной связи между показателями не существует.