Понятие дифференциала функции

Пусть функция y = f (х) дифференцируема на отрезке [ a, b ], содержащем некоторую точку x. Тогда производная в этой точке x определятся равенством . Из этого равенства (по теореме о связи функции, ее предела и бесконечно малой функции) следует, что

,

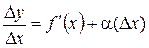где α(Δ x) – б.м.ф. при 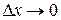. Отсюда

,

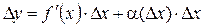то есть приращение ∆у функции f (х), дифференцируемой в точке х, можно представить в виде суммы двух слагаемых, которые являются бесконечно малыми:

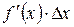– линейного члена относительно Δ x

и α(Δ x)· Δ x – нелинейного члена.

При этом первое слагаемое есть б.м.ф. одного порядка с Δ x, так как 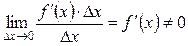, а второе слагаемое есть б.м.ф. более высокого порядка, чем Δ x, так как .

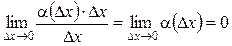Поэтому первое слагаемое 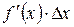называют главной частью приращения функции Δ y.

Определение. Главная часть приращения функции f (х), линейная относительно приращения независимой переменной ∆ х, называется дифференциалом функции f (х) в точке х, т.е. это произведение производной f' (x) на приращение независимой переменной ∆ х:

dy =df (x) =f' (х)·∆ х.

Замечание 1. Дифференциал функции составляет основную (главную) часть ее приращения, линейную относительно ∆х.

Например, приращение функции у = х ² в точке х = 1, вызванное приращением аргумента D х = 0,1, есть величина

∆у = (х + ∆х)² – х ² = (1 + 0,1)² – 1² = 0,21.

Дифференциал функции в этой точке равен

dy = f' (х) · ∆ х = 2 · х · ∆х = 2 · 1 · 0,1 = 0,2.

Таким образом, на нелинейную часть приращения α(Δ x) · ∆х приходится величина 0,01 из полной величины приращения 0,21.

Замечание 2. Дифференциал аргумента совпадает с его приращением (dх =∆ х), поэтому дифференциал функции записывается в виде

dy = df (х) = f' (x) dx,

т.е. дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Пример. Найти дифференциал функции f (x) = х.

Решение. df (x) = dx = х ' ∆ х = 1 · ∆ х = ∆ х.

Отсюда следует, что 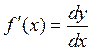, т.е. производную можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.

Геометрический смысл дифференциала: dy = KN (рис. 7), т.е. дифференциал функции f (х) в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получит приращение D х.

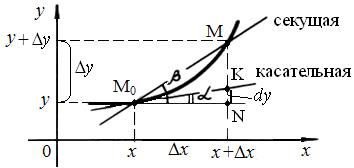
Рис. 7

При движении по графику функции f (х) из точки M ₀ в точку M абсцисса переходит из точки х в точку х + D х, а ордината получает приращение ∆у=f (х+∆х) – f (x). На рисунке это приращение ∆ у равно отрезку NM. Если же двигаться из точки х в точку х + D х по касательной, проведенной в точке М ₀, то ордината получит приращение, равное отрезку KN. Из треугольника М ₀ KN получим величину этого приращения: KN = М ₀ N ·tgα.

Так как tgα = f' (x), а М ₀ N = ∆ х, то KN = f' (x) · ∆ х и KM = α(Δ x) · D х.

Приращение функции ∆ y при малом приращении ∆x = dx по величине «очень мало» отличается от приращения по касательной, т.е. от дифференциала dy.

Так как касательная в точке М ₀ почти совпадает с кривой в малой окрестности точки х, то при ∆ х →0 разность (∆y – dy) = α(Δ x) · D х стремится к нулю быстрее, чем ∆ x. Дифференциал функции dy отличается от её приращения ∆y на бесконечно малую величину более высокого порядка по сравнению с ∆ x. Это обстоятельство используется в приближенных вычислениях.