Пусть в некотором промежутке определена функция  . Зафиксируем
. Зафиксируем 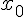 , принадлежащее этому промежутку.
, принадлежащее этому промежутку.
Дадим аргументу 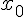 приращение
приращение 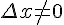 , так чтобы точка
, так чтобы точка 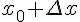 также принадлежала этому промежутку. При этом функция
также принадлежала этому промежутку. При этом функция  получит приращение
получит приращение
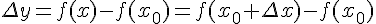 .
.
Составим отношение приращения функции к приращению аргумента:
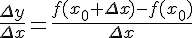
Найдем предел этого отношения при 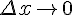 . Если этот предел существует, то его называют производной данной функции
. Если этот предел существует, то его называют производной данной функции 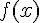 в точке
в точке 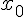 и обозначают
и обозначают 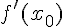 (читается "эф штрих от икс нулевого").
(читается "эф штрих от икс нулевого").
Таким образом,
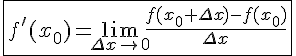 .
.
Определение. Производной данной функции  в точке
в точке 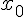 называется предел отношения приращения функции
называется предел отношения приращения функции 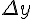 к приращению аргумента
к приращению аргумента 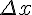 при стремлении
при стремлении 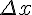 к нулю.
к нулю.
Пример 1. Дана функция 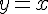 . Найти ее производную в произвольной точке
. Найти ее производную в произвольной точке 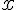 .
.
Решение:
Аргументу 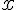 даем приращение
даем приращение 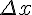 . Находим
. Находим 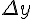 :
:
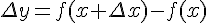 ,
,
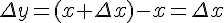
Составляем отношение 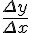 и находим предел этого отношения:
и находим предел этого отношения:
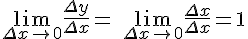 .
.
Таким образом, 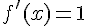 , т.е. производная функции
, т.е. производная функции 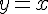 равна 1 в любой точке.
равна 1 в любой точке.
Ответ: 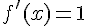 в любой точке.
в любой точке.
Пример 2. Найти производную функции 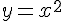 в произвольной точке
в произвольной точке 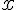 .
.
 2015-07-14
2015-07-14 1545
1545
