Точка 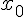 называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции  ,если существует такая окрестность точки
,если существует такая окрестность точки 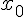 , что для всех
, что для всех 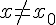 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 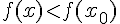 ,
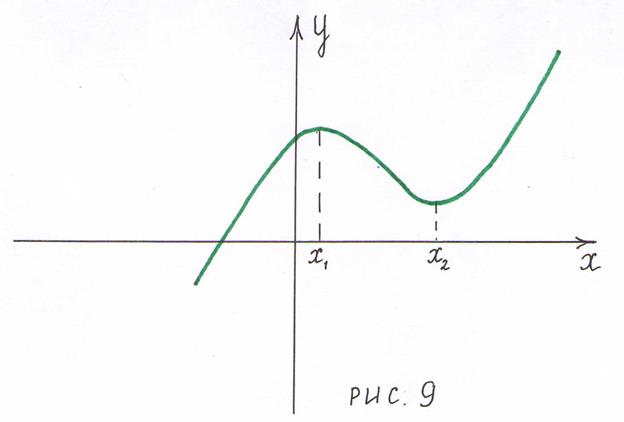
, 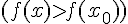 . На рис.9 изображены точки:
. На рис.9 изображены точки: 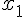 - точка максимума,
- точка максимума, 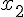 - точка минимума.
- точка минимума.
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Минимум или максимум функции называется экстремумом функции.
Рассмотрим условия существования экстремума функции.
Теорема 1. Необходимое условие экстремума функции.
Если дифференцируемая функция  имеет экстремум в точке
имеет экстремум в точке 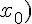 , то ее производная в этой точке равна нулю.
, то ее производная в этой точке равна нулю.
Геометрически равенство 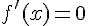 означает, что в точке экстремума дифференцируемой функции касательная к её графику параллельна оси
означает, что в точке экстремума дифференцируемой функции касательная к её графику параллельна оси 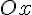 .
.
Из теоремы 1 вытекает следствие: если при всех рассматриваемых значениях 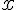 функция
функция  имеет производную, то она может иметь экстремум только при тех значениях, при которых производная обращается в нуль.
имеет производную, то она может иметь экстремум только при тех значениях, при которых производная обращается в нуль.
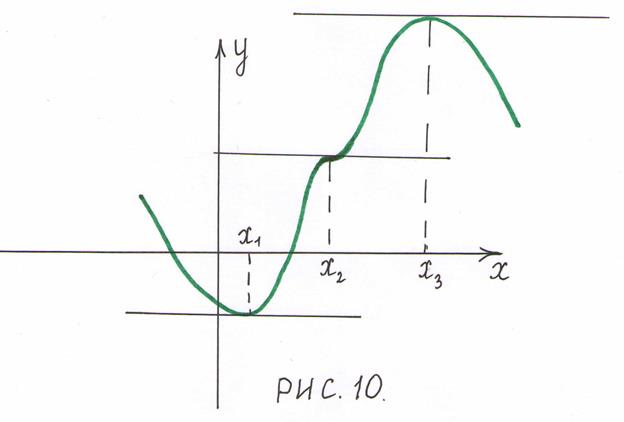
Обратное неверно: не при всяком значении 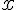 , при котором производная обращается в нуль, обязательно существует экстремум. На рис.10 изображен график функции, у которой при
, при котором производная обращается в нуль, обязательно существует экстремум. На рис.10 изображен график функции, у которой при 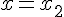 производная равна нулю (касательная параллельна оси
производная равна нулю (касательная параллельна оси 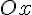 , но в этой точке функция не имеет экстремума.
, но в этой точке функция не имеет экстремума.
Рассмотрим точки в которых функция не является дифференцируемой (то есть не существует конечной производной).
В таких точках функция может иметь минимум или максимум, а может не иметь ни того, ни другого.
Например, функция 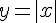 не имеет производной в точке
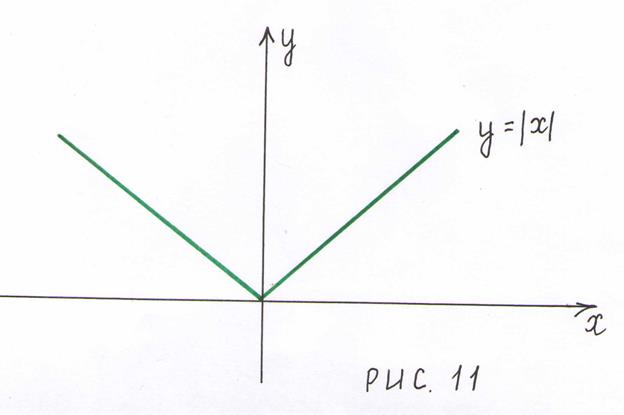
не имеет производной в точке 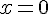 , но в этой точке данная функция имеет минимум. (рис. 11).
, но в этой точке данная функция имеет минимум. (рис. 11).
Функция 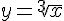 не имеет конечной производной в точке
не имеет конечной производной в точке 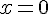 (касательной является ось
(касательной является ось 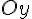 ). В этой точке функция не имеет ни максимума, ни минимума. (рис.12).
). В этой точке функция не имеет ни максимума, ни минимума. (рис.12).
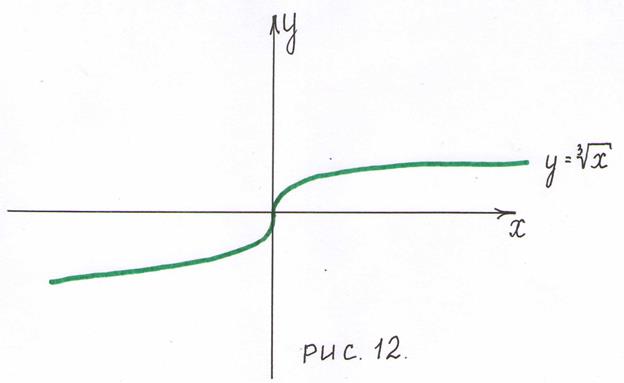
Таким образом, непрерывная функция может иметь экстремум в точках, в которых производная равна нулю или не существует. Такие точки называются критическими.
Теорема 2. Достаточное условие экстремума.
Если непрерывная функция  дифференцируема в некоторой окрестности критической точки
дифференцируема в некоторой окрестности критической точки 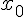 и при переходе через эту точку слева направо производная
и при переходе через эту точку слева направо производная 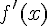 меняет знак с плюса на минус, то
меняет знак с плюса на минус, то 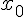 - точка максимума, а если с минуса на плюс, то
- точка максимума, а если с минуса на плюс, то 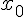 - точка минимума.
- точка минимума.
Правило исследования функции  на экстремум:
на экстремум:
1. Найти критические точки функции  , то есть точки, в которых производная функции равна нулю
, то есть точки, в которых производная функции равна нулю 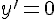 или не существует.
или не существует.
2. Выбрать из них лишь те, которые являются внутренними точками области определения функции.
3. Определить знак производной слева и справа от каждой из выбранных критических точек.
4. В соответствии с достаточными условиями экстремума выписать точки экстремума и вычислить значения функции в этих точках.
Пример. Найти точки экстремума функции 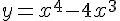 и значения функции в этих точках.
и значения функции в этих точках.
Решение. Область определения функции – вся числовая прямая.
Находим производную данной функции и приравниваем ее к нулю: 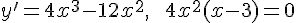 . Решая это уравнение, получаем
. Решая это уравнение, получаем 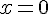 и
и 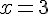 - критические точки (необходимое условие экстремума
- критические точки (необходимое условие экстремума 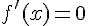 выполнено).
выполнено).
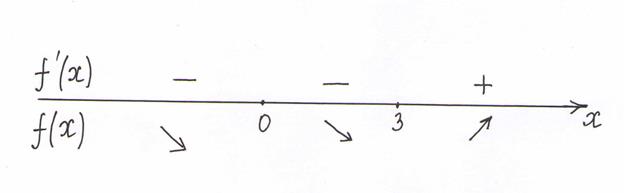
Проверяем выполнение достаточного условия экстремума. Рассмотрим точку 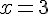 . Слева от этой точки
. Слева от этой точки 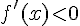 , например,
, например, 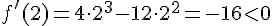 , справа от нее
, справа от нее 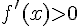 , например,
, например, 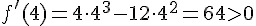 . Следовательно, достаточные условия экстремума выполняются, и точка
. Следовательно, достаточные условия экстремума выполняются, и точка 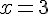 является точкой минимума. Находим значение функции в точке минимума:
является точкой минимума. Находим значение функции в точке минимума: 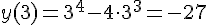 .
.
Теперь рассмотрим точку 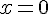 . Слева от этой точки
. Слева от этой точки 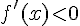 , справа
, справа 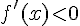 , Следовательно, достаточное условие экстремума не выполняется и точка
, Следовательно, достаточное условие экстремума не выполняется и точка 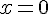 не является точкой экстремума.
не является точкой экстремума.
Ответ: 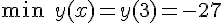
Вопрос. Производная функции  равна
равна 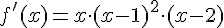 . Какая из критических точек не является точкой экстремума?
. Какая из критических точек не является точкой экстремума?
Начало формы
| все точки являются точками экстремума | |
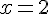 | |
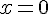 | |
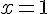 |
 2015-07-14
2015-07-14 30129
30129
