Пусть функция  определена на множестве
определена на множестве 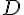 и пусть множество
и пусть множество 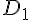 принадлежит множеству
принадлежит множеству 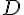 . Если для любых значений
. Если для любых значений 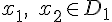 из неравенства
из неравенства 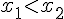 вытекает неравенство:
вытекает неравенство:
1. 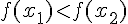 , то функция
, то функция  называется возрастающей на множестве
называется возрастающей на множестве 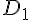 ;
;
2. 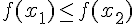 , то функция
, то функция  называется неубывающей на множестве
называется неубывающей на множестве 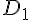 ;
;
3. 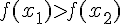 , то функция
, то функция  называется убывающей на множестве
называется убывающей на множестве 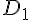 ;
;
4. 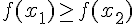 , то функция
, то функция  называется невозрастающей на множестве
называется невозрастающей на множестве 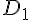 .
.
Возрастающие, убывающие, невозрастающие и неубывающие функции на множестве 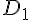 называются монотонными на этом множестве, а возрастающие и убывающие - строго монотонными.
называются монотонными на этом множестве, а возрастающие и убывающие - строго монотонными.
Достаточные условия возрастания и убывания функции: Если функция  дифференцируема на интервале
дифференцируема на интервале 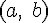 и
и 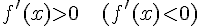 для любых
для любых 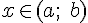 , то эта функция возрастает (убывает) на заданном интервале.
, то эта функция возрастает (убывает) на заданном интервале.
<!--[endif]-->
Если 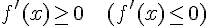 для любых
для любых 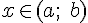 , то функция не убывает (не возрастает) на этом интервале.
, то функция не убывает (не возрастает) на этом интервале.
Пример. Найти интервалы возрастания и убывания функции 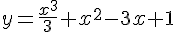 .
.
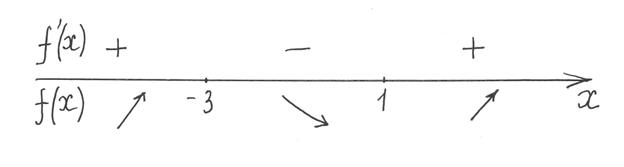
Решение. Область определения функции – вся числовая прямая. Находим производную функции 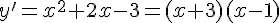 . Методом интервалов находим интервалы знакопостоянства производной.
. Методом интервалов находим интервалы знакопостоянства производной.
Из неравенства 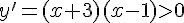 следует, что функция возрастает при всех значениях
следует, что функция возрастает при всех значениях 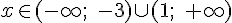 ;
;
а из неравенства 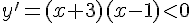 следует, что функция убывает на интервале
следует, что функция убывает на интервале 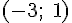 .
.
Вопрос. Функция 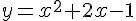 возрастает на интервале:
возрастает на интервале:
Начало формы
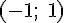 | |
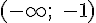 | |
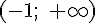 | |
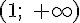 |
 2015-07-14
2015-07-14 3572
3572
