Найдем разложение функции 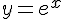 по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки 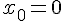 . Находя последовательно производные от этой функции, получим:
. Находя последовательно производные от этой функции, получим:
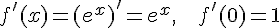 ,
,
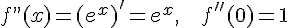 ,
,
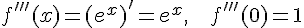 ,
,

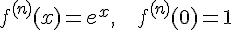 .
.
Находим значение 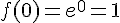
Подставим полученные значения в формулу Тейлора:
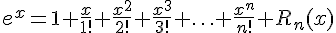 ,
,
где 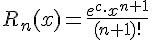 - остаточный член в форме Лагранжа.
- остаточный член в форме Лагранжа.
При 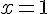 получим формулу, позволяющую найти приближенное значение числа
получим формулу, позволяющую найти приближенное значение числа 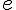 :
:
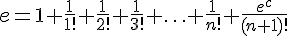 .
.
Так как 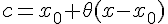 ,
, 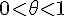 , то при
, то при 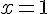 и
и 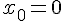 получим
получим 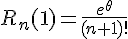
Если задана погрешность 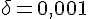 , то подберем
, то подберем 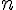 таким образом, чтобы
таким образом, чтобы 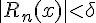 .
.
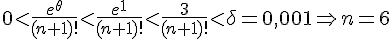 .
.
Таким образом, 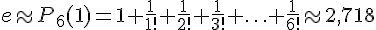 .
.
Найдем разложение функции 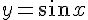 в окрестности точки
в окрестности точки 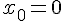 по формуле Тейлора:
по формуле Тейлора:
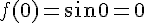 ,
,
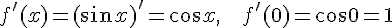 ,
,
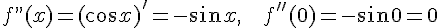 ,
,
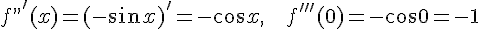 ,
,
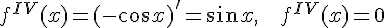 .
.
Таким образом, все производные четного порядка в точке 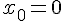 равны нулю, а производные нечетного порядка равны
равны нулю, а производные нечетного порядка равны 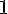 или
или 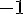 . Следовательно, разложение примет вид:
. Следовательно, разложение примет вид:
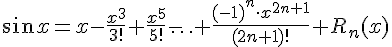 ,
,
где остаточный член в форме Лагранжа равен 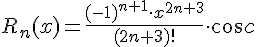 .
.
Используя полученное разложение, приближенно вычислим 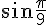 . При вычислении ограничимся первыми двумя членами разложения:
. При вычислении ограничимся первыми двумя членами разложения:
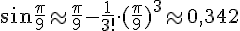 .
.
Приведем разложения по формуле Тейлора в окрестности точки 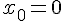 некоторых элементарных функций:
некоторых элементарных функций:
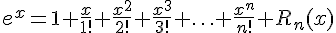
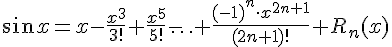
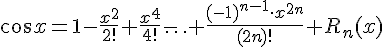 .
.
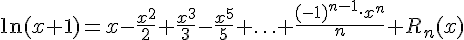 .
.
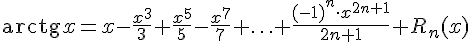 .
.
Формулу Тейлора при 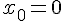 также называют формулой Макларена.
также называют формулой Макларена.
Вопрос. Разложение какой функции в окрестности точки 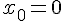 имеет вид
имеет вид
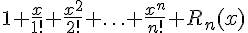 ?
?
Начало формы
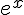 | |
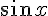 | |
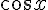 | |
 |
 2015-07-14
2015-07-14 5880
5880
