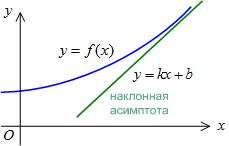
Определение. Асимптотой для кривой  называется прямая, расстояние до которой до точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой, т.е.
называется прямая, расстояние до которой до точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой, т.е. 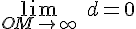 .
.
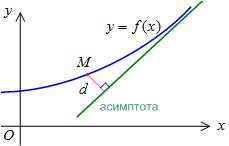
Асимптоты могут быть вертикальными, горизонтальными и наклонными.
Прямая  является вертикальной асимптотой, если
является вертикальной асимптотой, если
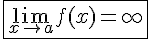 или,
или,
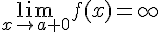 или
или 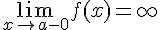 .
.
Для отыскания вертикальных асимптот необходимо найти те значения 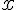 , при которых функция неограниченно возрастает или убывает. Обычно это точки разрыва второго рода.
, при которых функция неограниченно возрастает или убывает. Обычно это точки разрыва второго рода.
Пример 1. Найти вертикальные асимптоты графика функции 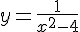 .
.
Решение. Знаменатель обращается в ноль в точках 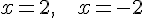 . Так как
. Так как 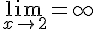 и
и 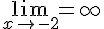 , следовательно, прямые
, следовательно, прямые 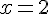 и
и 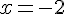 являются вертикальными асимптотами.
являются вертикальными асимптотами.
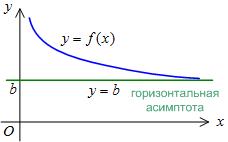
Прямая 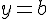 является горизонтальной асимптотой, если
является горизонтальной асимптотой, если 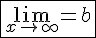 .
.
Для того, чтобы найти горизонтальную асимптоту, надо найти предел функции при 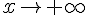 и
и 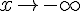 .
.
Пример 2. Найти горизонтальную асимптоту графика функции 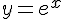 .
.
Решение. Находим предел 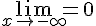 . Следовательно, горизонтальной асимптотой (причем влево) графика данной функции при
. Следовательно, горизонтальной асимптотой (причем влево) графика данной функции при 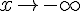 является прямая
является прямая 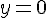 . Заметим, что
. Заметим, что 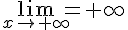 , поэтому горизонтальной асимптоты вправо не существует.
, поэтому горизонтальной асимптоты вправо не существует.
Уравнение наклонной асимптоты находится в виде 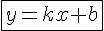 ,
,
где 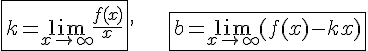 .
.
Пример 3. Найти наклонную асимптоту графика функции 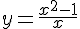 .
.
Решение. Находим угловой коэффициент асимптоты: 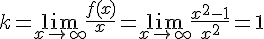 .
.
Далее вычисляем свободный член уравнения асимптоты:
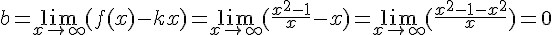 .
.
Таким образом, наклонной асимптотой графика данной функции является прямая 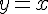 .
.
Вопрос. Горизонтальной асимптотой графика функции 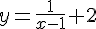 является прямая
является прямая
Начало формы
 | |
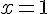 | |
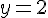 | |
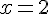 |
 2015-07-14
2015-07-14 3645
3645